1. 문제 풀이
1. 1874번 - 스택 수열
import sys
n = int(sys.stdin.readline())
stack = []
result = ''
idx = 1
flag = True
for i in range(n) :
num = int(sys.stdin.readline())
for j in range(idx, num+1):
stack.append(j)
result += '+\n'
idx += 1
if num == stack[-1] :
stack.pop()
result += '-\n'
else :
flag = False
break
if flag :
print(result)
else :
print('NO')스택 문제 풀이
풀이
1. 현재 입력 받은 수보다 작으면 그 수까지 +, stack에 넣어준다.
2. 스택의 마지막 값이 현재 입력 받은 수와 같다면 -, pop한다.
3. 만약 같지 않다면 수열 생성이 불가능 하므로 NO출력
2. Red-Black Tree 개념 공부
이진 탐색 트리(Binary Search Tree)의 한 종류
스스로 균형을 잡는 트리(self-balancing binary search tree) -> O(log n)
이진 트리의 특수한 형태로서, 컴퓨터 공학 분야에서 숫자 등의 비교 가능한 자료를 정리하는 데 쓰이는 자료구조
자료의 삽입과 삭제, 검색에서 최악의 경우에도 일정한 실행 시간을 보장한다(worst-case guarantees)
루트에서 리프까지의 경로에 나타나는 노드의 생깔을 제한함으로써 그러한 경로 중 어떠한 것도 다른 것의 2배 이상 길지 않음을 보장
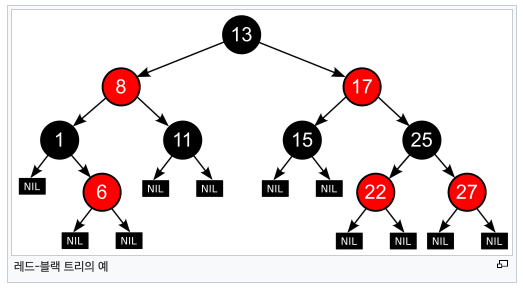
1. 속성
- 모든 노드는 red 또는 black이다.
- root = black
- nil node = 존재하지 않음을 의미하는 노드
- 자녀가 없을 때 자녀를 nil node로 표기한다.
- 값이 있는 노드와 동등하게 취급
- RB Tree에서 leaf node = nil node
- 모든 nil node = balck = 모든 leaf 노드는 black이다.
- sentinel node(경계 노드) : 모든 nil node, root node의 부모를 표현하도록 한다. → 메모리 절약
- red 의 자녀들을 반드시 black 이어야 한다.
- red가 연속적으로 존재할 수 없다.
- 임의의 노드에서 자손 nil node까지 가능 경로들의 black 수는 같다.(자기 자신은 제외)
- black height : 노드 x에서 임의의 자손 nil node까지 내려가는 경로에서의 black 수(본인 제외)
- 두 자녀가 같은 색을 가질 때 부모와 두 자녀의 색을 바꿔줘도 이 속성은 여전히 만족한다.
2. 삽입 동작
- 삽입 전 RB 트리 속성은 만족한 상태이다.
- 삽입 방식은 일반적인 BST와 동일하다.
- 삽입 후 RB 트리 위반 여부를 확인한다.
- RB트리 속성을 위반했다면 재조정한다.
1. 삽입하는 노드의 색은 항상 red이다.
: 삽입한 후에도 마지막 속성(balck height 조건)을 만족하기 위해서
2. 삽입한 노드가 root 노드일 경우 black으로 바꿔준다.

3. 부모 노드가 red, 자식 노드도 red 일 경우
▶ 옮길 수 있는 경우 : 색 변경 + BST 특징 유지하면서 Rotation


▶ 옮길 수 없는 경우 : 부모노드와 삼촌 노드의 색을 balck / 할아버지 노드 색을 red로 바꾼 후 할아버지 노드를 기준으로 다시 확인

★ 삽입 예제 - 25 삽입 후 속성 재조정 과정 ★
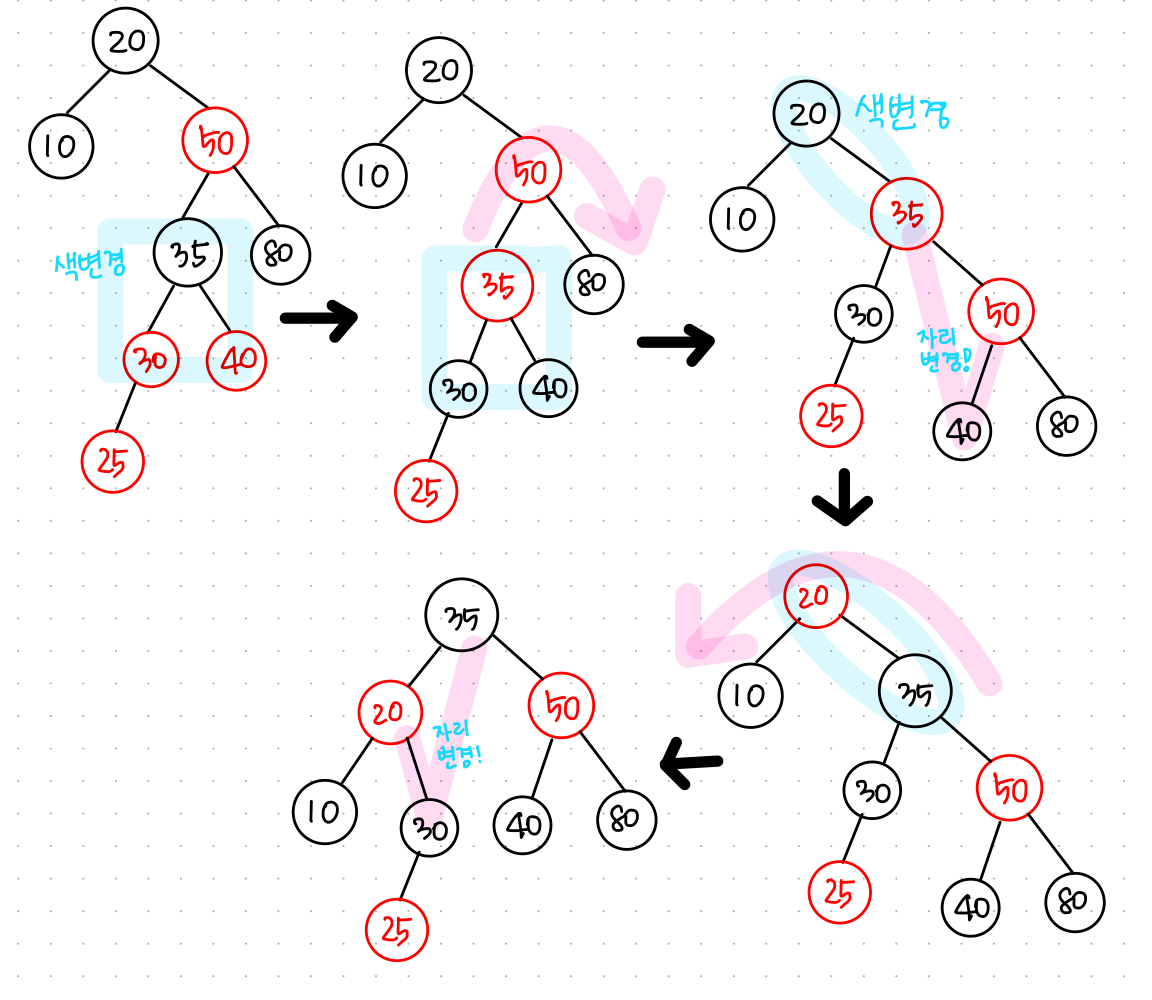
3. 삭제 동작
- 삭제 전 RB 트리 속성은 만족한 상태이다.
- 삭제 방식은 일반적인 BST와 동일하다.
- 삭제 후 RB 트리 위반 여부를 확인한다.
- RB트리 속성을 위반했다면 재조정한다.
1. 속성 위반 여부 확인
: 어떤 색이 삭제되는지가 매우 중요하다.
★ 삭제되는 색 ★
삭제하려는 노드의 자녀가 없거나 하나라면 → 삭제되는 노드의 색
삭제하려는 노드의 자녀가 둘이라면 → 삭제되는 노드의 successor의 색
+ successor : 선택한 노드의 오른쪽 서브트리 중 가장 작은 값을 가지는 노드
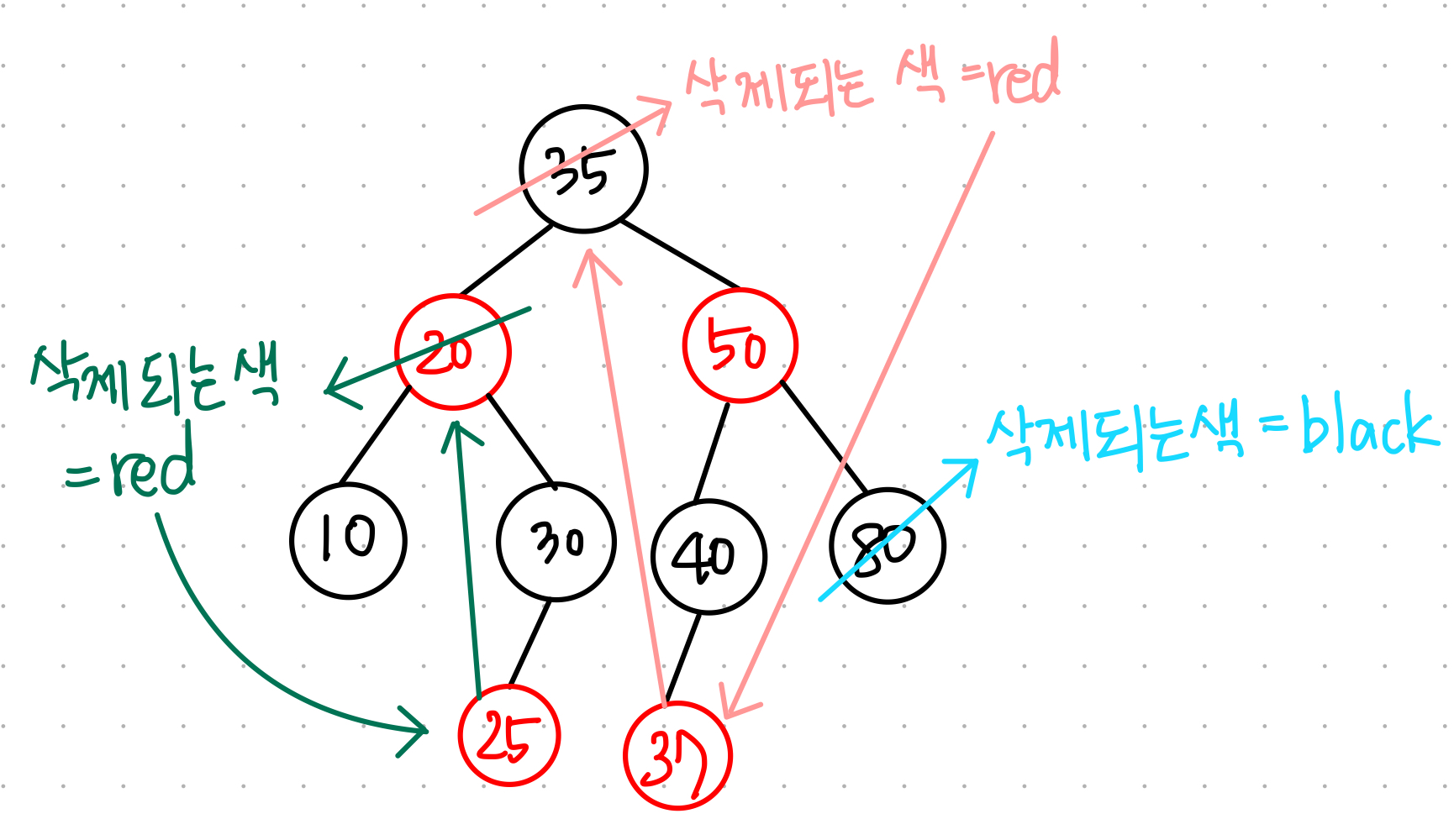
2. 삭제되는 색 = red 일 경우 어떤한 속성도 위반하지 않는다.
3. 삭제되는 색 = black
▶ 2번 속성 위반
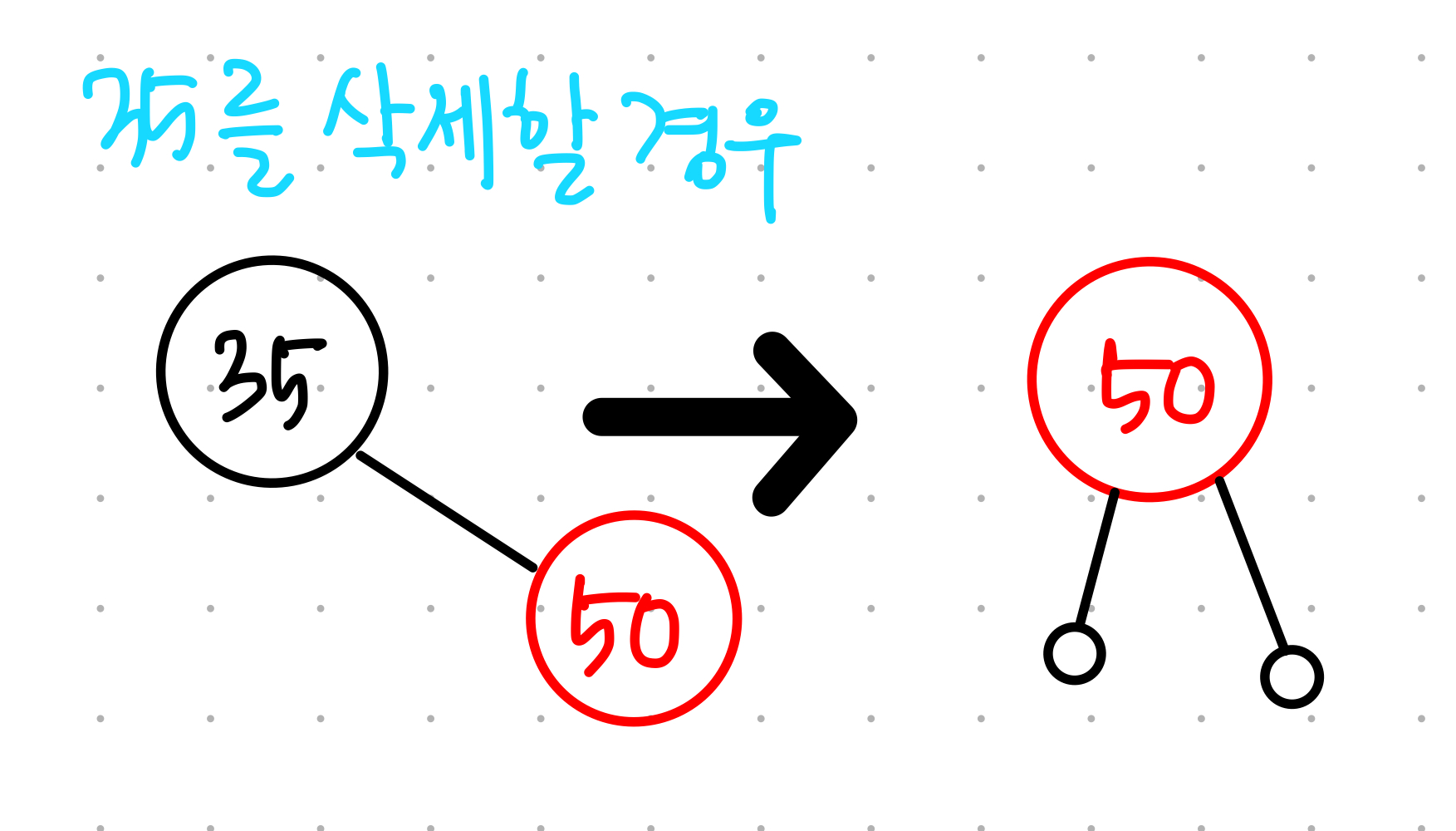
▶ 4번 속성 & 5번 속성 위반
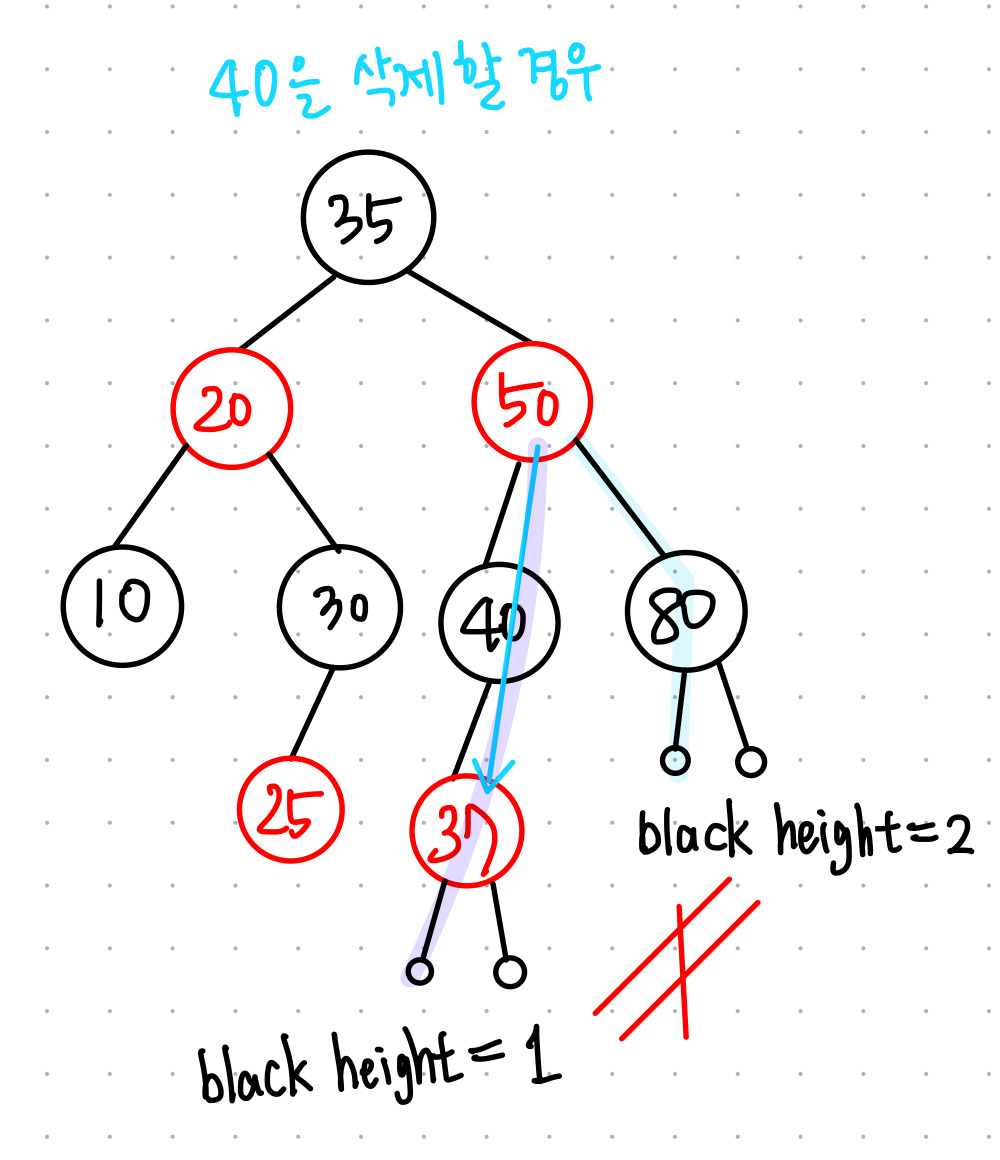
2. 속성 위반 재조정
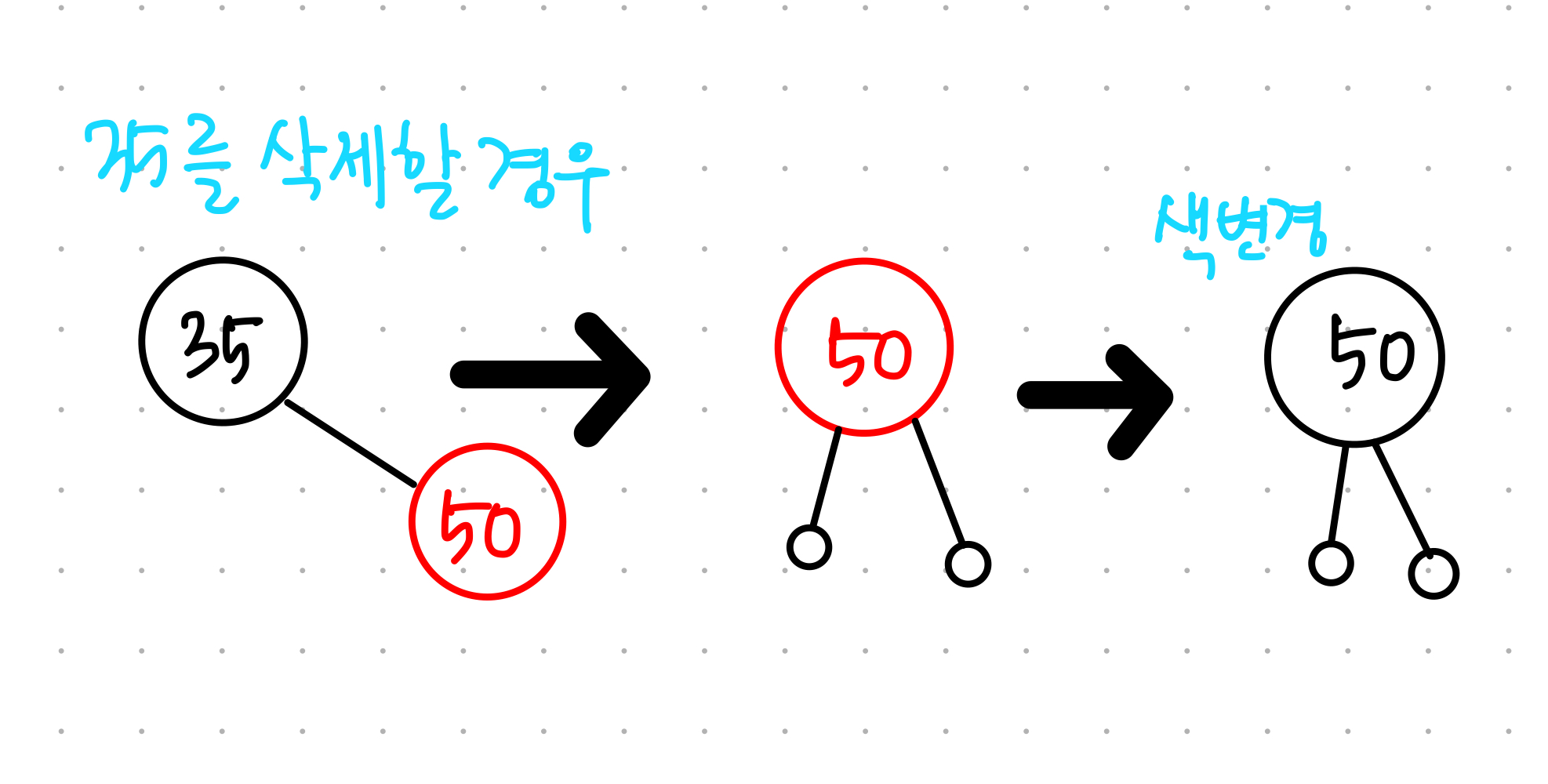
▶ 2번 속성 위반
: 루트 노드를 black으로 변경
▶ 4번 속성 & 5번 속성 위반
: 실제로 위와 같은 특수한 상황이 아니면 5번 속성 위반은 항상 발생
★ extra black ★
: 삭제된 색의 위치를 대체한 노드에 부여 / 경로에서 black 수를 count할 때 extra black은 하나의 balck으로 생각


3. extra black 해결하기
▶ red-and-black 해결하기
: red-and-black 을 black으로 바꿔주기
▶ doubly black 해결하기
기준 : doubly black의 형제의 색과 그 형제의 자녀들의 색
1. doubly black 의 오른쪽 형제 = black / 그 형제의 자녀의 오른쪽 = red

- 오른쪽 형제 = 부모의 색, 오른쪽 형제의 오른쪽 자녀, 부모 = black 변경
- 부모를 기준으로 왼쪽으로 회전
- 오른쪽 / 왼쪽 반대로 가능
2. doubly black의 오른쪽 형제 = black / 그 형제의 왼쪽 자식 = red / 그 형제의 오른쪽 자식 = black

- c와 b의 색을 서로 변경 후 b를 기준으로 오른쪽 회전
- 1번 경우가 완성되므로 1번 경우로 해결
3. doubly black의 오른쪽 형제 = black / 그 형제 자녀 모두 = black
: doubly black과 그 형제의 black을 모아서 부모에게 전달 → 부모가 extra black을 해결하도록 위임

- doubly black과 b의 blackd을 가지고 부모에게 위임
- 루트를 변경하여 다시 확인
4. doubly black의 오른쪽 형제 = red
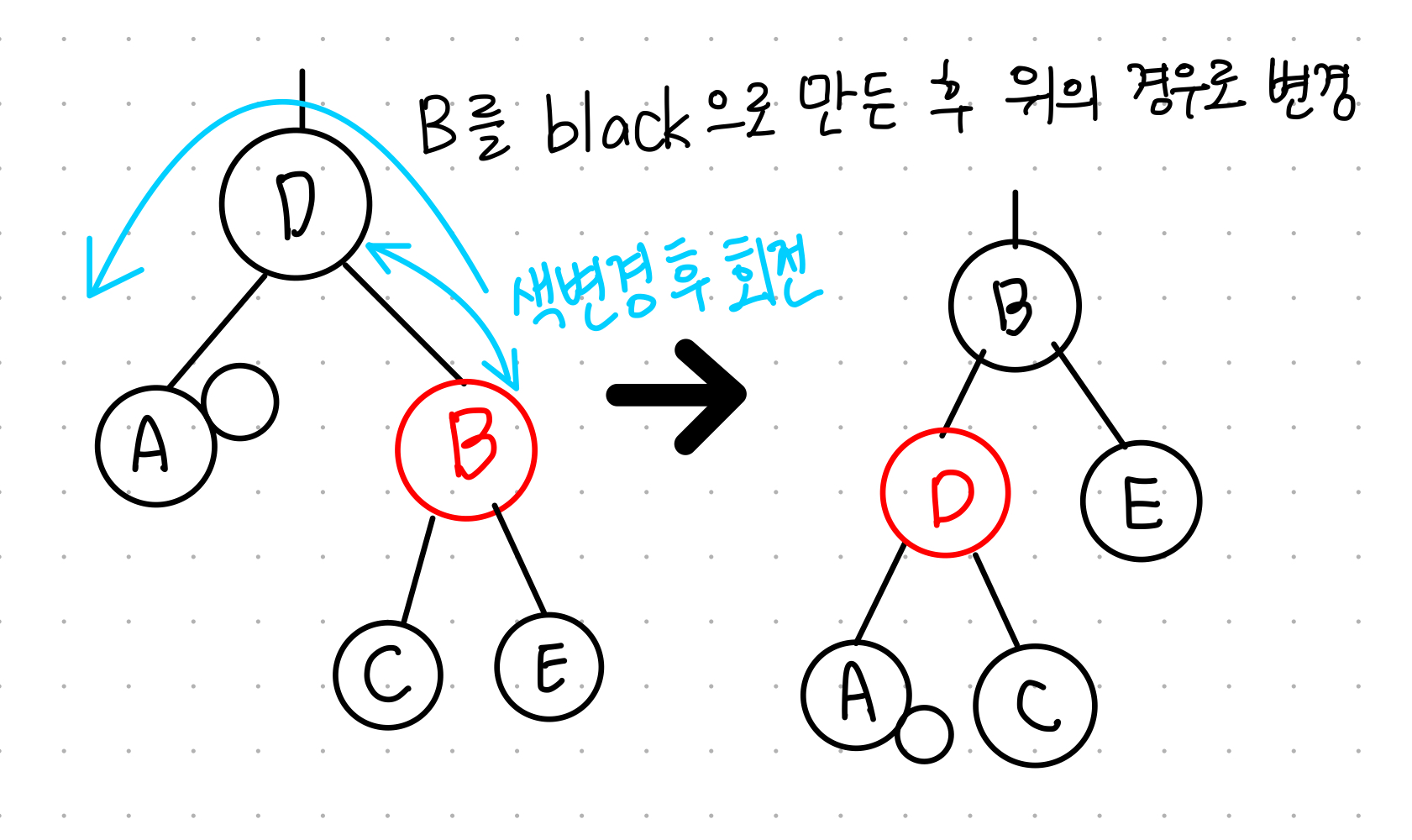
- b와 d의 색을 서로 변경하고 d를 기준으로 왼쪽 회전
- 위의 경우들 중 맞는 경우 선택
4. AVL Tree와 비교
: 삽입/삭제에서 AVL Tree 보다 Red-Black Tree가 더 빠르다. 검색 성능은 AVL Tree가 좀 더 빠르다.
→ AVL Tree 가 더 엄격한 균형 규칙을 적용
균형 잡는 방식
▶ AVL Tree : balance factor = {-1, 0, 1} 을 만족하도록 한다.
사용 사례) dictionary
▶ Red-Black Tree : red-black tree 속성을 만족하도록 한다.
사용 사례) linux kernel, java treemap 등
< 참고 >
🔗 강의 1부 : https://www.youtube.com/watch?v=2MdsebfJOyM
🔗 강의 2부 : https://www.youtube.com/watch?v=6drLl777k-E
🔗 https://en.wikipedia.org/wiki/Red–black_tree
🔗 https://ko.wikipedia.org/wiki/레드-블랙_트리
🔗 successor 개념 : https://vprog1215.tistory.com/74
3. 기계 수준 표현
1. 스택 데이터 저장과 추출
Stack 이란?
프로시저 호출을 처리하는데 중요한 역할을 한다.
후입선출(Last-In First-Out)
▶ 연산
1. push : 스택에 데이터를 추가
2. pop : 가장 최근에 추가된 값 제거
- 스택은 배열로 구현될 수 있다.
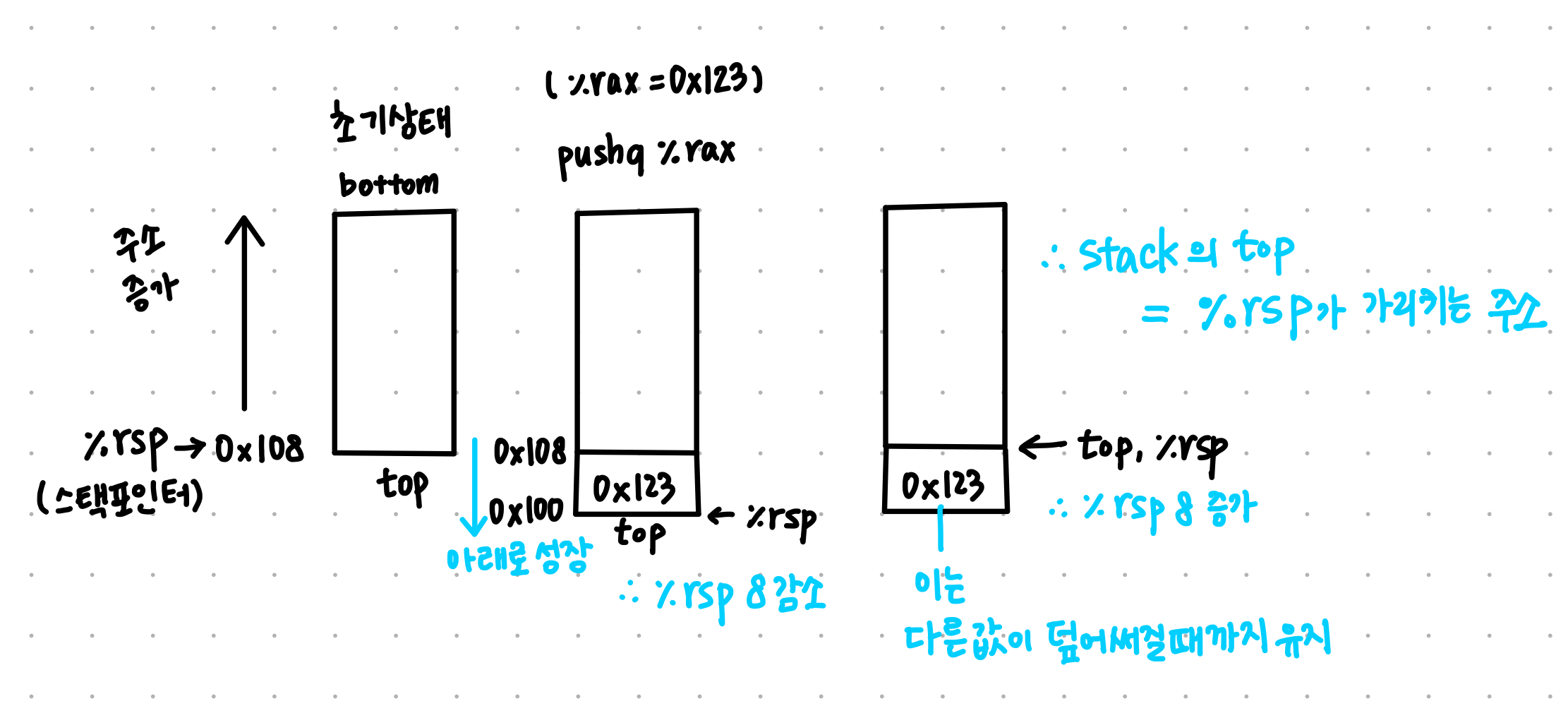
- 관습적으로 스택은 아래 방향으로 성장한다.
- top : 배열의 끝부분 / 스택의 원소 중 가장 낮은 주소를 갖는다.
- 스택 포인터 %rsp : 스택의 맨 위 원소 주소를 저장
- 스택 top = 스택 포인터가 가리키는 주소
- 스택 탑보다 윗부분에 저장된 값은 모두 무효인 값들이다.
- 연산자 - 1개의 operand 사용
- popq (추출을 위한 데이터 목적지): 데이터 추출
- movq (%rsp), %rax
- addq $8, %rsp
- pushq (추가할 소스 데이터): 스택에 데이터 추가
- subq $8, %rsp
- movq %rbp, (%rsp)
- q : quard word = 8byte
- popq (추출을 위한 데이터 목적지): 데이터 추출
'KraftonJungle2기 > Today I Learned' 카테고리의 다른 글
| [TIL] 기계 수준 표현3 + RB Tree 삽입 구현(코드X) (1) | 2023.05.08 |
|---|---|
| [TIL] Make란? + stack 문제 풀이 (0) | 2023.05.07 |
| [TIL] LinkedList & AVL Tree (with C) (1) | 2023.05.05 |
| [TIL] C언어 공부하기 (0) | 2023.05.04 |
| [TIL] 문제 풀이 연습 - two point (with python) (1) | 2023.05.03 |



