[graph] 깊이 우선 탐색(DFS, Depth First Search)

그래프 순회(Graph Traversal) 또는 그래프 탐색(Graph Search) 란?

하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한번씩 방문하는 것

---

깊이 우선 탐색(DFS, Depth First Search)

시작 정점에서 한 방향으로 갈 수 있는 가장 먼 경로까지 깊이 탐색해가다가 더 이상 갈 곳이 없으면 가장 마지막에 만났던 간선이 있는 정점으로 되돌아와서 다른 방향의 간선으로 탐색을 계속함으로써 모든 정점을 방문하는 순회방법

마지막 갈림길로 되돌아가야하므로 후입선출(Last-IN-First-Out) 구조인 스택(Stack) 사용

사실상 백트래킹과 똑같은 개념을 사용한다.

---

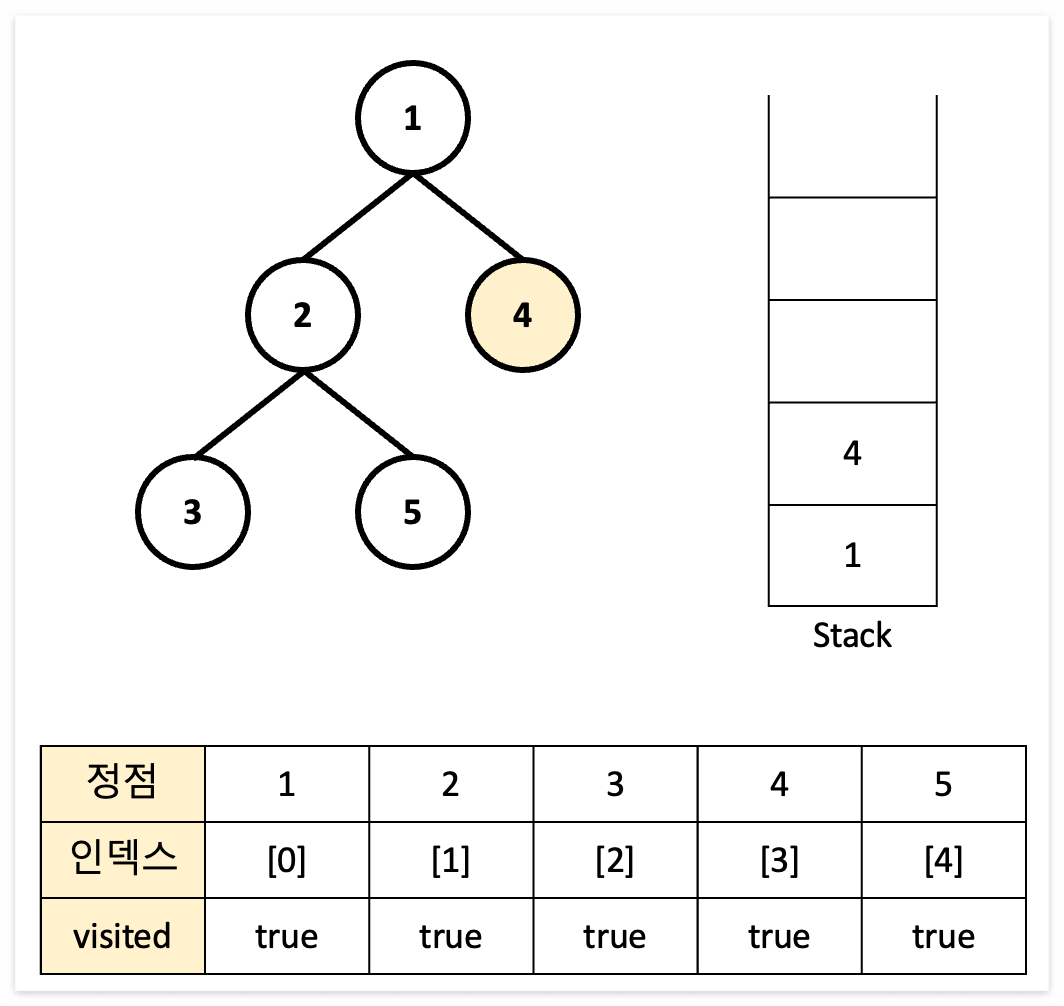
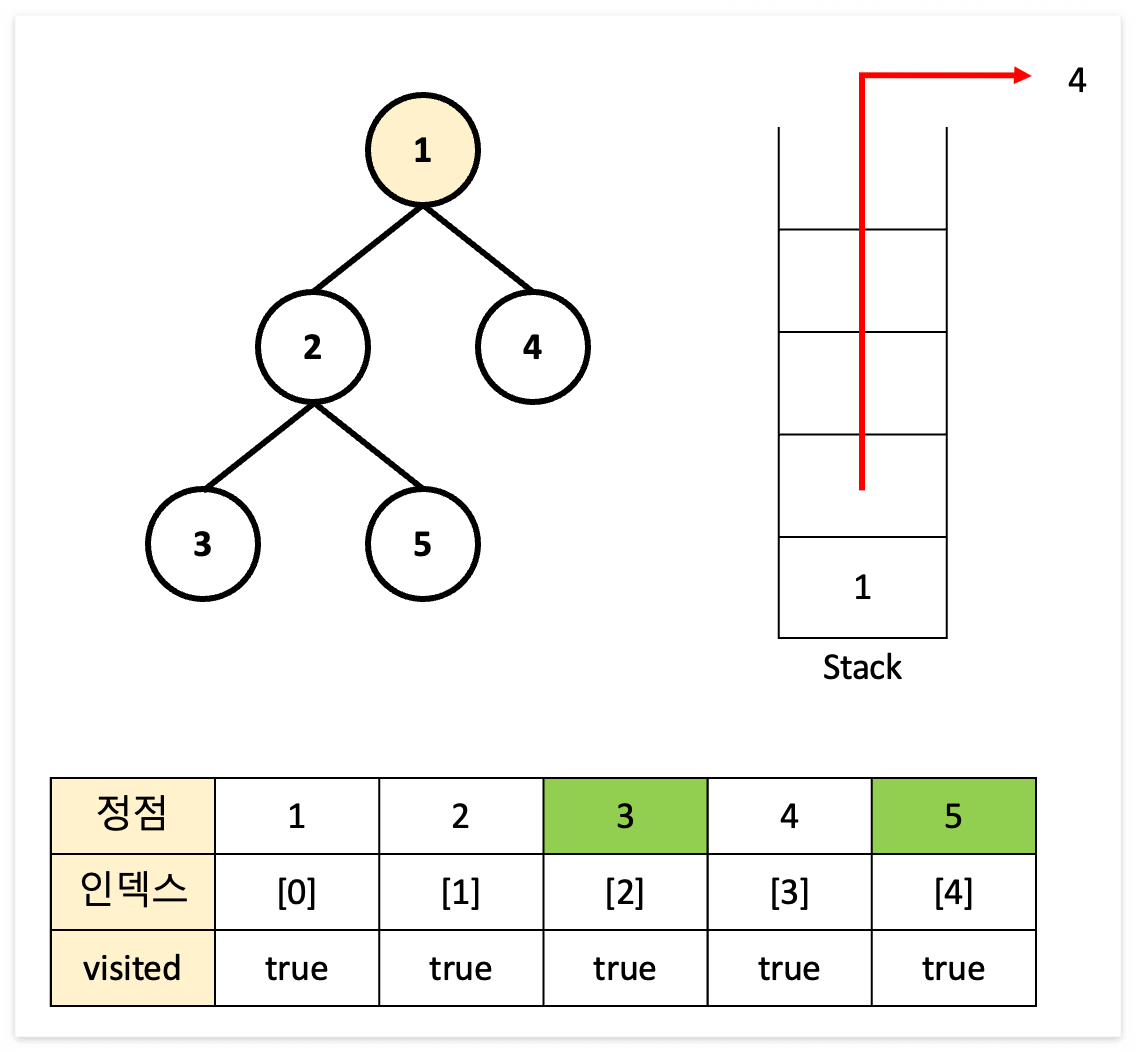
DFS 수행 순서

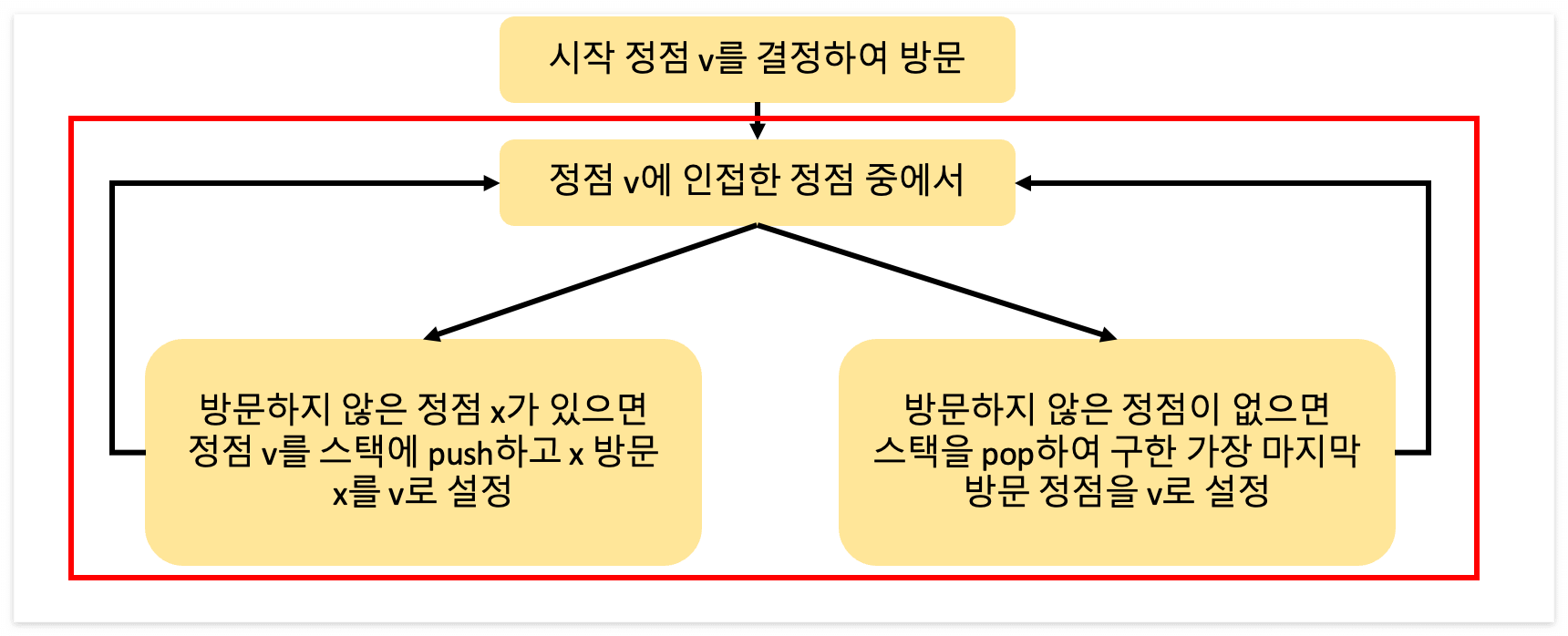
스택이 공백이 될 때까지 빨간 상자 부분을 반복한다.

---

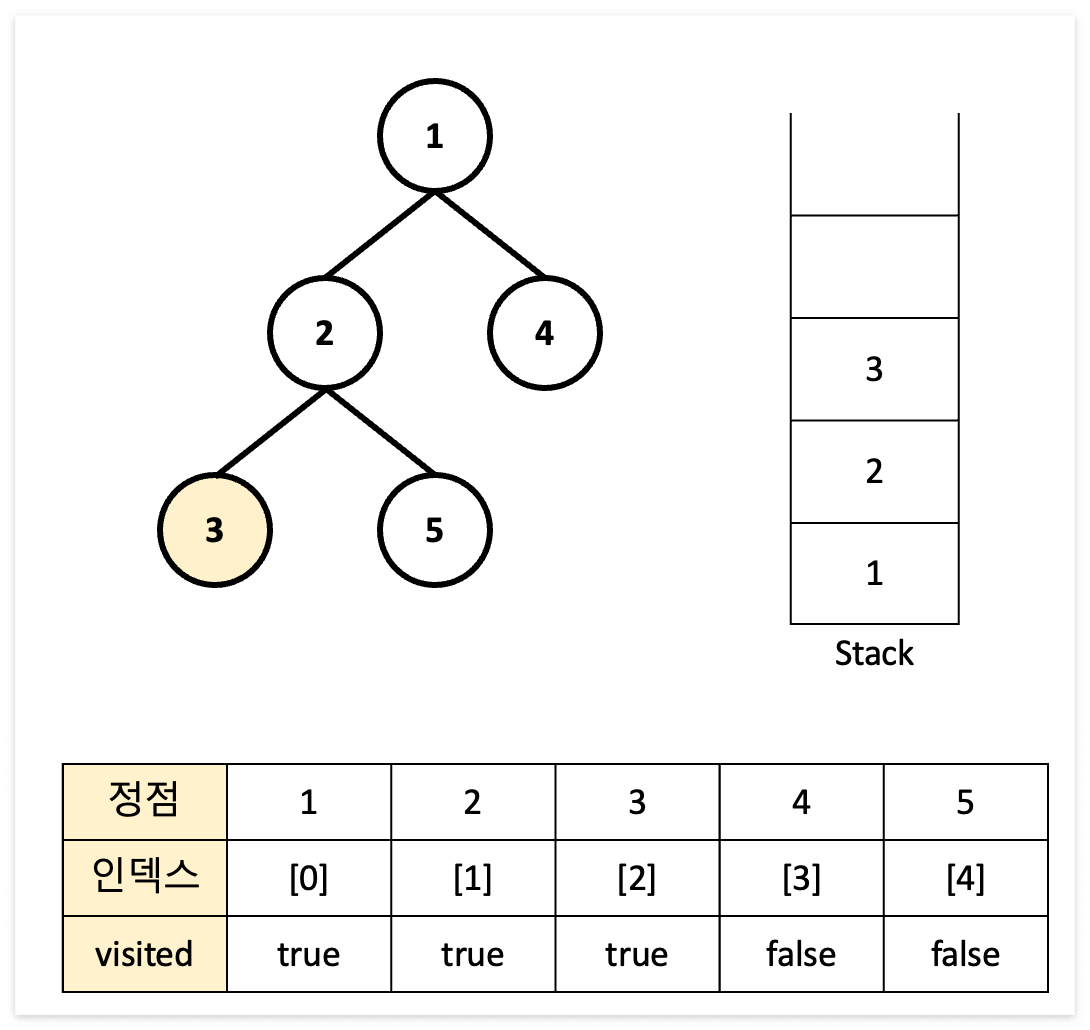
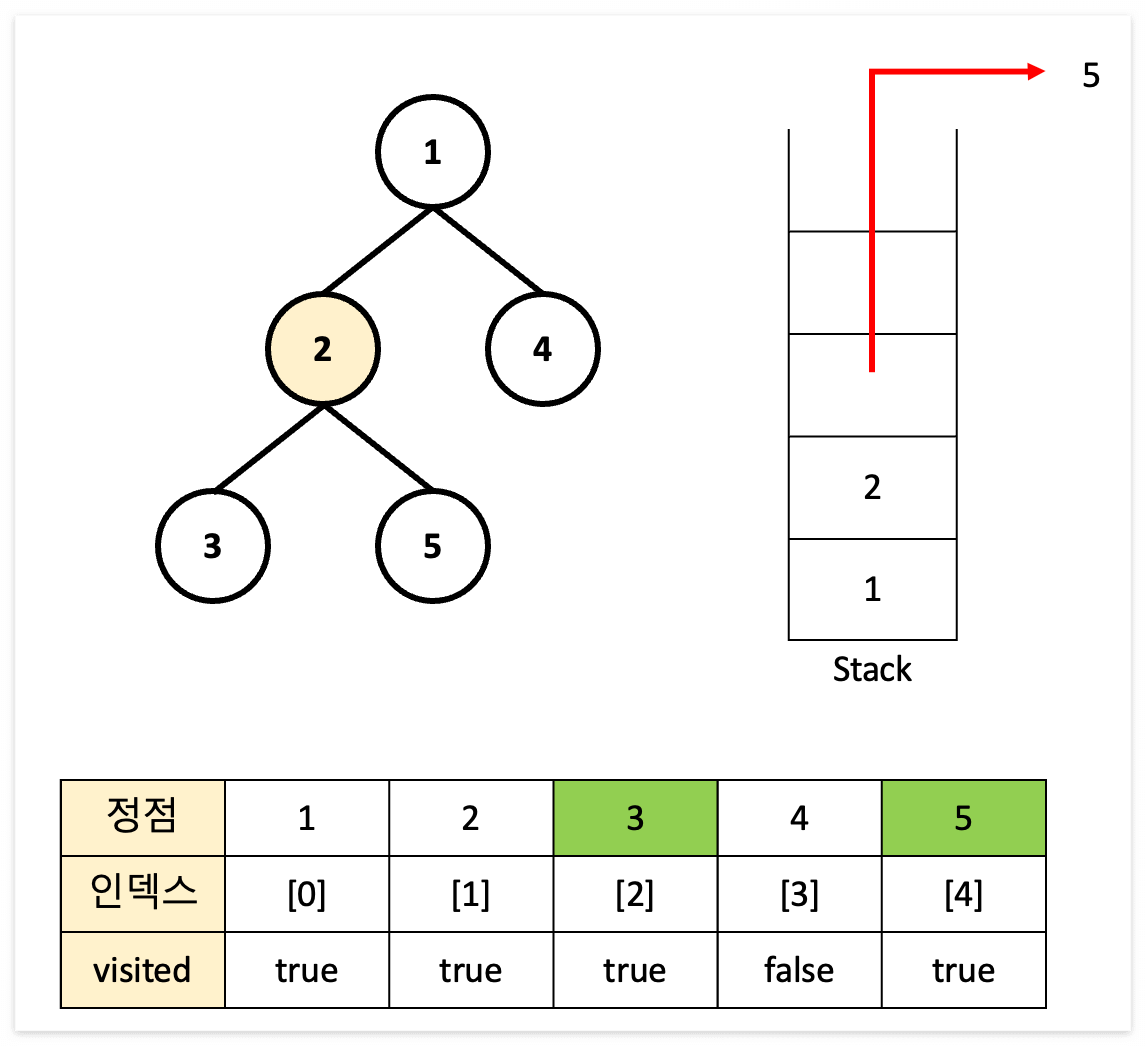
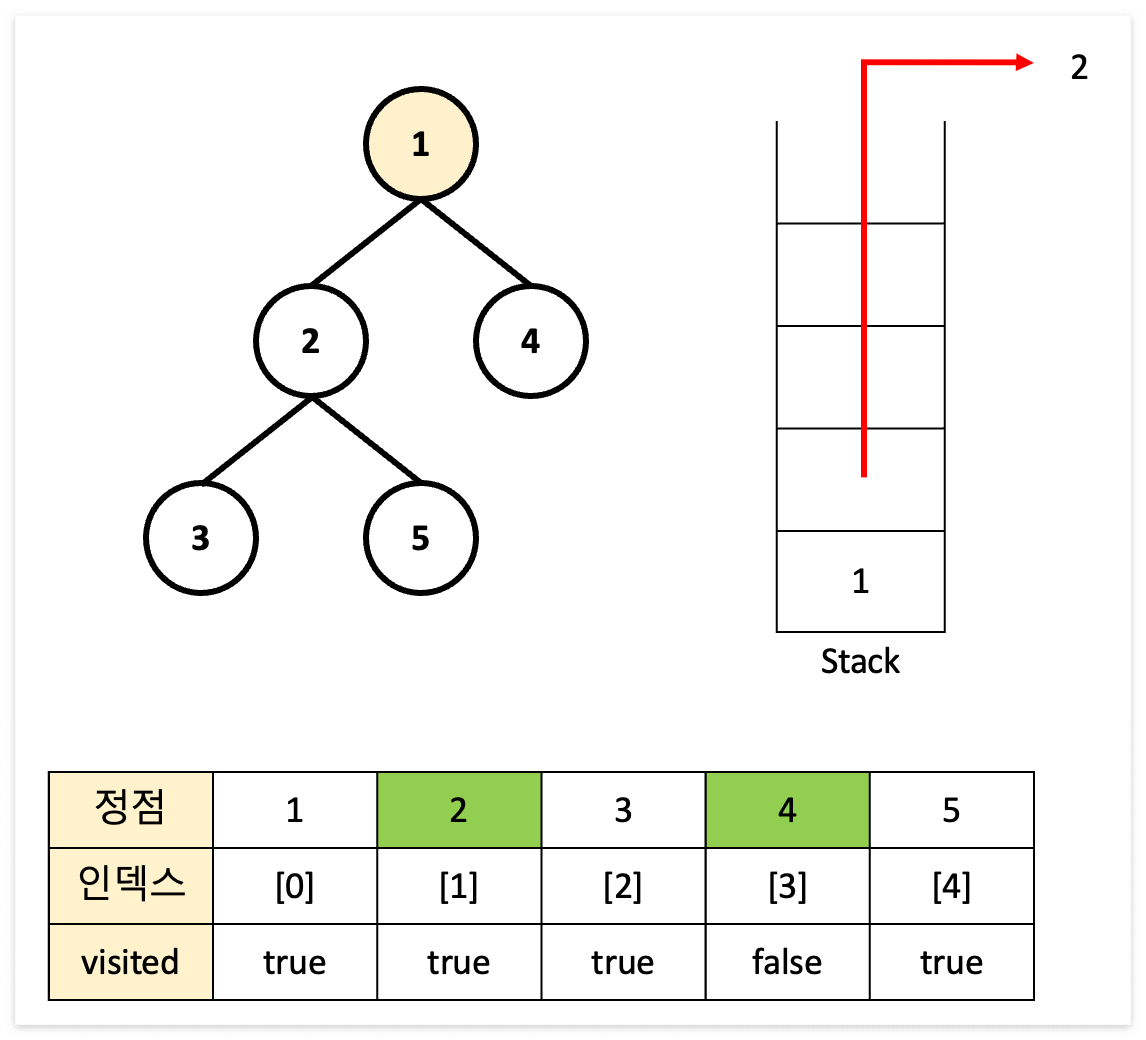
DFS 과정 표현

초기 상태

↓

시작 정점 1 탐색 시작

↓

1의 인접 정점2 방문

↓

2의 인접 정점3 방문

↓

3에서 더 탐색할 정점이 없으므로 pop()  →  현재 정점 = 2

↓

2의 인접 정점 중 방문하지 않는 정점5 방문

↓

5에서 더 탐색할 정점이 없으므로 pop()  →  현재 정점 = 2

↓

2에서 더 탐색할 정점이 없으므로 pop()  →  현재 정점 = 1

↓

1의 인접 정점 중 방문하지 않는 정점4 방문

↓

4에서 더 탐색할 정점이 없으므로 pop()  →  현재 정점 = 1

↓

1에서 더이상 탐색할 정점이 없으므로 pop() → 스택이 비었으므로 탐색 종료

↓

결과 : 1 → 2 → 3 → 5 → 4

---

인접 행렬로 구현한 그래프 DFS

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;
import java.util.StringTokenizer;

public class DFS_matrix {
    static void DFS(int[][] graph, int v) {
        //스택을 이용안 DFS
        Stack<Integer> stack = new Stack<>();
        boolean visited[] = new boolean[graph.length]; // 방문 여부를 검사할 배열

        //처음 검사할 노드 = v
        stack.push(v);
        visited[v] = true;
        System.out.print("DFS 탐색 순서 : " + v);

        //더 탐색할 인접정점이 없으면 false
        //즉, 현재 정점에서 모든 인접 정점을 방문했거나 인접 정점이 존재하지 않으면 false
        boolean flag = false;

        while(!stack.isEmpty()) {
            /**
             * peek() 연산은 스택의 top 부분에 있는 값을 스택에서 삭제하지 않고 반환해주는 연산
             * w = 현재 탐색 중인 정점
             */
            int w = stack.peek();
            flag = false; //while문 반복시 false로 초기화

            for(int i = 1; i < graph.length; i++) {
                //w의 인접 정점이 존재하고 그 정점 i를 방문하지 않았으면
                if(graph[w][i] == 1 && !visited[i]) {
                    stack.push(i);
                    visited[i] = true;
                    System.out.print(" -> " + i);
                    
                    //w에 인접정점이 존재하므로 ture로 변경해준다.
                    flag = true;
                    
                    /**
                     * break 사용이유
                     * 1. for문 탈출
                     * 2. flag = ture 이므로 밑의 코드 실행 안함
                     * 3. 즉, while문을 반복하도록 만든다
                     *      -> 스택에 i를 push 해놓았으므로  다음 w = i가 된다.
                     */
                    break;
                }
            }
            //위의 for문에서 탐색했을 때 flag가 변경되지 않았다는 것
            //현재 노드 w 에서 더이상 탐색할 노드가 없으므로 스택에서 제거
            if(!flag) {
                stack.pop();
            }
        }
    }
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(bf.readLine()); //정점의 수
        int M = Integer.parseInt(bf.readLine()); //간선의 수

        int[][] graph = new int[N+1][N+1]; //그래프 인접 행렬로 구현
        StringTokenizer st;
        for(int i = 0; i < M; i++){
            st = new StringTokenizer(bf.readLine());
            int x = Integer.parseInt(st.nextToken());
            int y = Integer.parseInt(st.nextToken());
            //무방향 그래프
            graph[x][y] = 1;
            graph[y][x] = 1;
        }
        DFS(graph, 1);
    }
}

위의 코드 실행 결과

---

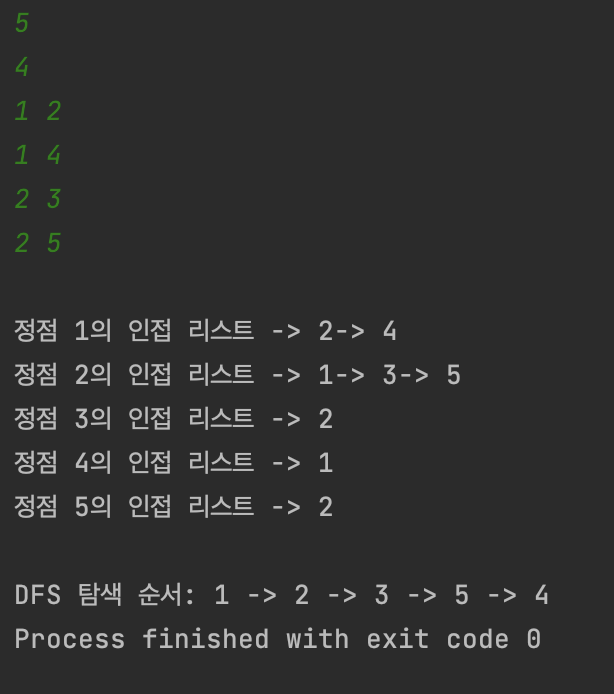
인접 리스트로 구현한 그래프 DFS

GitHub - ChoSooBeen/graph: graph - data structure study code

 

    public void DFS(int v, int n) { // v = 시작 정점, n = 정점의 수
        Stack<Integer> stack = new Stack<>();
        boolean visited[] = new boolean[n+1];

        // 탐색 시작 정점 v
        stack.push(v);
        visited[v] = true;
        System.out.print("DFS 탐색 순서: " + v);

        while (!stack.isEmpty()){
            gNode w = head[v]; //현재 탐색하고 있는 정점

            /**
             * w == null 이라는 것 = head[v] 리스트는 전부 탐색을 완료했다는 것
             * 즉, while 문이 종료되었다는 것은 현재 스택의 가장 위에 있는 값은 사용 완료했다는 의미이다.
             */
            while(w != null) {
                if(!visited[w.vertex]) { //방문한 적이 없다면
                    stack.push(w.vertex);
                    visited[w.vertex] = true;
                    System.out.print(" -> " + w.vertex);
                    v = w.vertex;
                    w = head[v];
                }
                else { //방문한 적이 있으면 다음 인접 정점으로 이동
                    w = w.link;
                }
            }
            //사용완료한 값(=가장 위의 값)은 제거하고
            stack.pop();
            //스택이 비어있지 않다면 현재 스택의 가장 위의 값을 v로 저장한다.
            if(!stack.isEmpty()) {
                v = stack.peek();
            }
        }
    }

위의 코드 실행 결과