728x90
★ 정점의 개수 n개 , 모서리의 개수 m개 ★
그래프를 구성하는 정점에 대해서 두 정점을 연결하는 간선의 유무를 저장하는 방법
n X n 이차원 배열(정점의 수에 대한 정방행렬)을 사용하여 두 정점 사이에 간선이 존재하면 1, 존재하지 않으면 0으로 저장한다.
이때, 하나의 정점에서 자기 자신으로 간선(=자체 간선)은 존재할 수 없으므로 행렬의 대각선 값은 항상 0
무방향 그래프의 경우 행렬의 (i, j)와 (j,i)의 값이 같으므로 대각선을 중심으로 대칭을 이룬다.

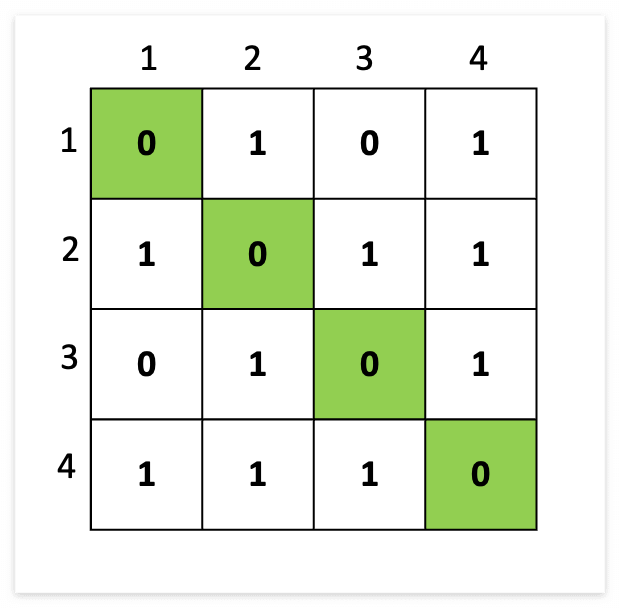
무방향 그래프에서 행 i의 합 = 열 i의 합 = 정점 i의 차수
ex) 정점 2의 차수 = 2행의 합(=1+0+1+1) = 2열의 합(=1+0+1+1) = 3
JAVA로 구현한 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine()); //정점의 수
int M = Integer.parseInt(bf.readLine()); //간선의 수
//인접행렬로 그래프 구현 - 0번 인덱스 사용X
int[][] graph = new int[N+1][N+1];
StringTokenizer st;
for(int i = 0; i < M; i++){
st = new StringTokenizer(bf.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
//무방향 그래프이므로 양쪽 다 저장
graph[x][y] = 1;
graph[y][x] = 1;
}
}
}
| 장점 | (i,j)의 인덱스로 바로 접근할 수 있어 모서리를 추가하거나 제거하는 작업이 매우 빠르다. |
| 단점 | 항상 nXn개의 메모리를 사용해야 하므로 (정점의 개수 > 모서리의 개수) 일 경우 메모리 낭비 문제가 발생한다. |
728x90
'자료구조 > Graph' 카테고리의 다른 글
| [graph] 깊이 우선 탐색(DFS, Depth First Search) (0) | 2023.03.06 |
|---|---|
| [graph] 인접 리스트로 방향 그래프 구현하기 (0) | 2023.03.04 |
| [graph] 인접 리스트로 무방향 그래프 구현하기 (2) | 2023.03.04 |
| [graph] 인접 배열로 방향 그래프 구현하기 (0) | 2023.03.04 |
| [graph] 기본 개념 정리 (0) | 2023.03.03 |



