728x90
1. 스택 연습 문제 (10000번 - 원 영역)
import sys
# https://wonyoung2257.tistory.com/79 참고
N = int(sys.stdin.readline())
circles = []
for i in range(N) :
x, r = map(int, sys.stdin.readline().split())
circles.append((x-r, '(')) # 중점을 기준으로 왼쪽에 있는 좌표
circles.append((x+r, ')')) # 중점을 기준으로 오른쪽에 있는 좌표
# x좌표 순으로 오름차순 정렬 & 같을 경우 ')' 문자를 가진 값이 앞으로 오도록
# 아스키 코드 : '(' = 72, ')' = 73
circles.sort(key = lambda x: (x[0], -ord(x[1])))
# {좌표, 괄호모양, 상태값}
# 상태값 = 0 : 뒤의 원과 접해 있지 않는다. / 1 : 뒤의 원과 접한다.
stack = []
result = 1
# 왼쪽, 오른쪽 저장을 따로 했기에 N*2번 반복
for i in range(N*2) :
x, y = circles[i] # x: 좌표, y: 괄호
# 스택이 비어있을 경우에는 무조건 push
if len(stack) == 0 :
stack.append({'x' : x, 'y' : y, "status" : 0})
# 스택에 값이 존재할 경우
else :
# 괄호가 ')' 이면 원이 무조건 완성
if y == ')' :
# 원이 다른 원과 접해있지 않을 경우
if stack[-1]['status'] == 0 :
result += 1
# 원이 다른 원과 접해있을 경우
elif stack[-1]['status'] == 1 :
result += 2
# 앞에 사용한 '(' 값 pop
stack.pop()
#현재 완성된 원이 다음 원과 접해있는지 확인
if i != N*2-1 :
if circles[i+1][0] != x :
stack[-1]['status'] = 0
# 괄호 '('일 경우
else :
# 접해있을 경우 상태 변경
if stack[-1]['x'] == x :
stack[-1]['status'] = 1
stack.append({'x' : x, 'y' : y, "status" : 0})
print(result)- 스택의 특성을 이용하여 원을 ( ) 로 표현
- 문제에서의 조건 : 원은 서로 교차하지 않는다. 하지만, 접할 수는 있다.
- 위의 조건을 통해 2가지 경우의 수가 존재한다. → 코드상에서 상태값으로 표현
- 접해 있을 경우 : 위/아래로 영역이 나누어질 수 있다.
- 접하지 않았을 경우 : 나누어지지 않는다.
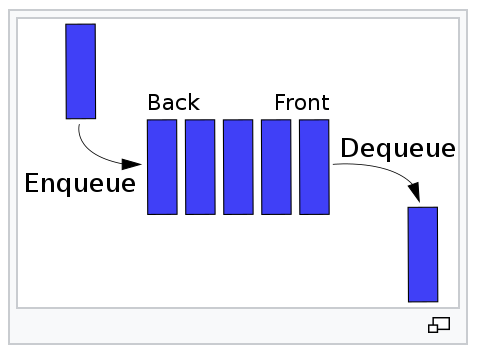
2. 큐(Queue)
스택과 같이 데이터를 임시저장하는 자료구조로 선입선출(First-In First-Out) 방식
- Enqueue : 큐에 데이터를 추가하는 작업, 리어(Rear) = Back → 데이터를 넣는 쪽
- Dequeue : 큐에서 데이터를 꺼내는 작업, Front → 데이터를 꺼내는 쪽
1. 리스트로 큐 구현하기
# 파이썬에서 큐도 간단히 리스트로 구현가능
queue = []
# queue에 값 추가하기
queue.append(1)
queue.append(2)
queue.append(3)
print("queue에 삽입한 후 : ",queue)
# queue에서 값 제거하기
print("첫번째 pop : ",queue.pop(0))
print("pop한 후 큐 : ", queue)
print("두번째 pop : ",queue.pop(0))
print("pop한 후 큐 : ", queue)
print("세번째 pop : ",queue.pop(0))
print("pop한 후 큐 : ", queue)이와 같이 큐를 리스트로 구현하면 pop(0)을 한 후에 리스트에 있는 값을 인덱스 1번 부터 앞으로 옮겨주는 추가 작업이 필요하다.
그래서 Dequeue를 할 때 원소를 옮기지 않기 위해 Ring Buffer를 사용하여 구현할 수 있다.
2. Ring Buffer로 큐 구현하기
원형 버퍼란?
: 고정된 크기의 버퍼를 양 끝이 연결된 것처럼 사용할 수 있게 해주는 자료구조
<출처> https://ko.wikipedia.org/wiki/원형_버퍼
# ring buffer를 이용한 fixedQueue 구현하기
class FixedQueue :
# 비어있는 큐에 deque(), peek() 함수를 호출할 때 내보내는 예외처리
class Empty(Exception) :
pass
# 가득 차있는 큐에 enque() 함수를 호출할 때 내보내는 예외처리
class Full(Exception) :
pass
# 초기화함수
def __init__(self, capacity) :
self.no = 0 # 큐에 쌓여있는 데이터 개수
self.front = 0 # 맨 앞의 원소 인덱스
self.rear = 0 # 맨 뒤의 원소 인덱스
self.capacity = capacity # 큐의 최대 크기
self.que = [None] * capacity # 큐의 배열
# 큐에 추가한 데이터 개수 반환
def __len__(self) :
return self.no
# 큐가 비어있으면 True, 아니면 False
def isEmpty(self) :
return self.no <= 0
# 큐가 차 있으면 True, 아니면 False
def isFull(self) :
return self.no >= self.capacity
# 큐에 데이터 삽입
def enque(self, x) :
if self.isFull() :
raise FixedQueue.Full
self.que[self.rear] = x
self.rear += 1
self.no += 1
if self.rear == self.capacity :
self.rear = 0
# 큐 맨 앞의 데이터 제거하여 반환
def deque(self) :
if self.isEmpty() :
raise FixedQueue.Empty
x = self.que[self.front]
self.front += 1
self.no -= 1
if self.front == self.capacity :
self.front = 0
return x
# 큐 맨 앞의 데이터 확인
def peek(self) :
if self.isEmpty() :
raise FixedQueue.Empty
return self.que[self.front]
# 큐애 value와 같은 데이터가 포함되어 있는 위치 반환, 없으면 -1
def find(self, value) :
for i in range(self.no) :
index = (i + self.front) % self.capacity
if self.que[index] == value :
return index
return -1
# 큐에 들어있는 value와 같은 데이터 개수 반환
def count(self, value) :
c = 0
for i in range(self.no) :
if self.que[(i + self.front) % self.capacity] == value :
c += 1
return c
# 큐에 value가 들어있으면 True, 아니면 False
def __contains__(self, value) :
return self.count(value)
# 큐 안에 모든 데이터를 비움
def clear(self) :
self.no = self.front = self.rear = 0
# 큐 안에 데이터 모두 출력
def dump(self) :
if self.isEmpty() :
print("Queue is Empty!")
else :
for i in range(self.no) :
print(self.que[(i + self.front) % self.capacity], end=' ')
print()3. 덱 (deque)
deque(double-ended queue)?
: 맨 앞과 맨 끝 양쪽에서 데이터를 모두 삽입, 삭제할 수 있는 자료구조
두 개의 포인터를 사용하여 양쪽에서 삽입 삭제 가능, 큐와 스택을 합친 형태라고 생각하면 된다.
python : collections.deque 로 제공한다.
기본적으로 python에서는 리스트로도 큐를 구현할 수 있지만 pop(0) 함수를 실행할 때 작업량이 많아진다.
왜냐하면 맨 앞의 값을 빼고 나머지 1번부터 맨 뒤까지의 값을 앞으로 한칸씩 옮겨줘야 하기 때문이다.
그러므로 이는 시간복잡도가 O(n)이다.
그러나 덱 같은 경우는 popleft()라는 함수를 사용하여 맨 앞의 값을 제거하는데
이는 앞에서도 뒤에서도 모두 삽입, 삭제가 가능한 자료구조라 시간복잡도는 O(1)이다.
그래서 기본적으로 python에서 pop(0)와 같은 동작이 필요하면 덱을 더 많이 사용하는 편이다.
1. deque를 이용한 문제 (18258번 - 큐2)
from collections import deque
import sys
N = int(sys.stdin.readline())
queue = deque()
def isEmpty() :
if len(queue) == 0 :
return 1
return 0
for _ in range(N) :
command = list(sys.stdin.readline().split())
if command[0] == "push" :
queue.append(command[1])
elif command[0] == "pop" :
if isEmpty() == 1 :
print(-1)
else :
print(queue.popleft())
elif command[0] == "size" :
print(len(queue))
elif command[0] == "empty" :
print(isEmpty())
elif command[0] == "front" :
if isEmpty() == 1 :
print(-1)
else :
print(queue[0])
else :
if isEmpty() == 1 :
print(-1)
else :
print(queue[-1])2. 2164번 - 카드2
import sys
from collections import deque
N = int(sys.stdin.readline())
def final_card(N) :
queue = deque(i for i in range(1, N+1))
flag = True
while len(queue) > 1 :
if flag :
queue.popleft()
flag = False
else :
queue.append(queue.popleft())
flag = True
print(queue.popleft())
final_card(N)import sys
from collections import deque
N, K = map(int, sys.stdin.readline().split())
def josephus(n, k) :
queue = deque(i for i in range(1, n+1))
result = []
count = 1
while queue :
if count == k :
result.append(queue.popleft())
count = 1
else :
queue.append(queue.popleft())
count += 1
print('<', end='')
for i in range(n-1) :
print(f'{result[i]}, ', end='')
print(f'{result[-1]}>')
josephus(N, K)4. 3190번 - 뱀
import sys
from collections import deque
##############input 값 정리###################################
N = int(sys.stdin.readline()) #보드의 크기
array = [[0] * (N+1) for _ in range(N+1)] # 문제에서 나온 보드는 (1,1) 부터 시작
L = int(sys.stdin.readline()) #사과의 개수
for _ in range(L) :
tmp_x, tmp_y = map(int, sys.stdin.readline().split())
array[tmp_x][tmp_y] = 1 # 사과 저장
K = int(sys.stdin.readline()) #방향 전환 횟수
v = {} # {시간 : 방향}
for _ in range(K) :
t, c = sys.stdin.readline().split()
v[int(t)] = c
##############################################################
# 뱀이 살아있는 시간 구하는 함수
def dummy() :
###############초기값 설정##################################
# 우 -> 하 -> 좌 -> 상
x = [1, 0, -1, 0]
y = [0, 1, 0, -1]
# 게임 시간
time = 0
# 초기 방향
d = 0
# 뱀의 초기 위치
current_x, current_y = 1, 1
# 뱀이 있는 곳
snake = deque([(current_x, current_y)])
###########################################################
while True :
current_x, current_y = current_x + x[d], current_y + y[d]
# 움직인 좌표값이 범위 내에 존재하고(즉, 벽에 부딪히지 않고) 자기 몸과 부딪히지 않으면
if 0 < current_x <= N and 0 < current_y <= N and (current_x, current_y) not in snake:
# x : 행 -> 좌우 움직여야 한다.
# y : 열 -> 위아래 움직여야 한다.
# 이차원 배열에 입력을 할 때 주의해야 함
if array[current_y][current_x] != 1 : # 현재 위치에 사과가 존재하지 않으면
a, b = snake.popleft()
array[b][a] = 0
snake.append((current_x, current_y))
time += 1
# 현재 시간이 방향을 바꿔야할 시간이라면
if time in v.keys() :
if v[time] == 'D' : # 오른쪽으로 돌아야 할 경우 +1
d = (d+1) % 4
else : # 왼쪽으로 돌아야 할 경우 -1
d = (d-1) % 4
else :
# 미리 종료 여부를 검사하고 나오기 때문에 마지막 1초를 더해준다.
return time + 1
print(dummy())이번 큐 관련 문제는 크게 어려운 점이 없었다.
그러나 마지막 뱀 문제에서 알고리즘에 대한 어려움보다 이차원배열의 인덱스에서 많이 헤매었다.
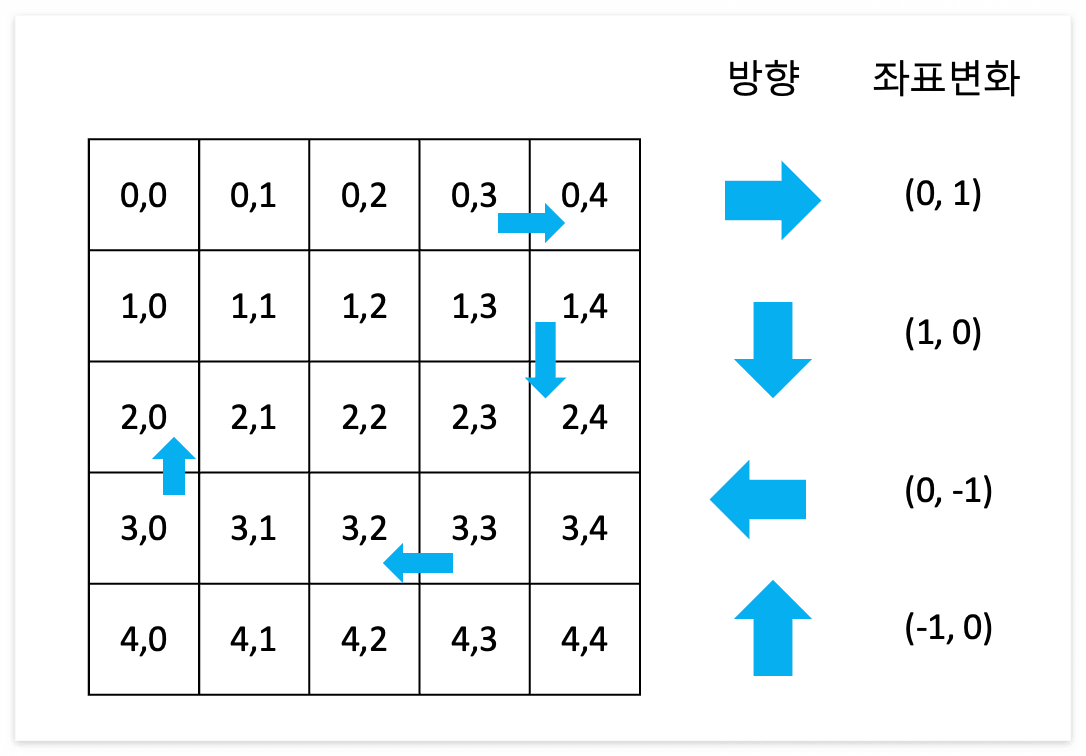
위의 이미지에서 보면 명확하게 볼 수 있다. 그러나 코드를 작성할 때 x는 행 y는 열 이라고 생각하고 그냥 배열에 [x][y]를 입력했다.
★ 어느 하나의 행에서 움직인다는 것은 좌우로 움직인다는 의미 ★
★ 어느 하나의 열에서 움직인다는 것은 위아래로 움직인다는 의미 ★
즉, 우리가 이차원 배열에 접근할 때는 위와 같이 코드를 작성했다면 배열[y][x] 로 접근해야 올바른 값이다.
3. Hashing
Hash Table 이라는 기억공간을 할당하고 해시함수(Hash Function)을 이용하여 레코드 키에 대한 hash table 내의 주소를 계산한 후 주어진 레코드를 해당 기억장소에 저장하거나 검색 작업을 수행하는 방식
- Hash Function: 데이터의 효율적 관리를 목적으로 임의의 길이의 데이터 → 고정된 길이 데이터로 매핑하는 함수
- key : 매핑 전 원래 데이터 값
- Hash value : 매핑 후 데이터 값
- Hashing : 매핑하는 과정

1. Hash Table
Hash map 또는 해시 표
: 해시함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 색인(index) 혹은 주소 삼아 데이터의 값(value)을 키와 함께 저장하는 자료구조
◆ bucket(버킷), slot(슬록) : 데이터가 저장되는 곳

▶ 장점
- 적은 리소스로 많은 데이터를 효율적으로 관리
- index 에 해시값을 사용함으로써 모든 데이터를 살피지 않아도 검색과 삽입, 삭제를 빠르게 수행
- 해시 함수는 언제나 동일한 해시값 리턴해 해시테이블의 크기에 상관없이 데이터에 대단히 빠르게 접근
- index는 계산이 간단한 함수로 작동 즉, 해시는 삽입, 삭제, 탐색시 계산복작섭 = O(1) 지향
- 키와 해시값 사이에 직접적인 연관이 없어 해시값만을 가지고 키를 온전히 복원하기 힘들어 보안면에서도 널리 사용
- 길이가 서로 다른 입력 데이터에 대해 일정한 길이의 출력을 만들 수 있어 데이터 축약 기능도 수행
▶ 단점
- Collision(해시 충돌) : 해시함수는 해쉬값의 개수보다 대개 많은 키값을 해시값으로 변환(many-to-one)하기 때문에 해시함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 낼 수 있다.

위와 같이 해시 충돌이라는 단점이 있지만 앞에서 공부한 직접 주소 테이블 방식보다 장점도 훨씬 많고 해시 충돌이라는 문제를 해결하기 위한 효율적인 방법이 존재한다. 물론 이상적인 해결법은 충돌을 완전히 피하는 것이지만 위에서 말한 것처럼 훨씬 더 많은 키 값을 해시값으로 변환하고 있기에 완전히 피하는 것은 불가능하다. 그래도 적절한 해시 함수를 선택하여 충돌을 피하거나 횟수를 줄여야한다.
이에 대해서는 다음에 더 이어서 공부해야 겠다.
참고 블로그 : https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/
728x90
'KraftonJungle2기 > Today I Learned' 카테고리의 다른 글
| [TIL] 자료구조 - 우선순위 큐 (0) | 2023.04.17 |
|---|---|
| [TIL] 백준 풀이 정리2 (0) | 2023.04.16 |
| [TIL] Algorithm - 분할정복 + 스택 (0) | 2023.04.14 |
| [TIL] Algorithm - 이분탐색(Binary Search) + 직접 주소 테이블이란? (1) | 2023.04.13 |
| [TIL] 백준 풀이 정리 (0) | 2023.04.12 |


