728x90
1. 우선순위 큐(Priority Queue)
우선순위 큐는 추상적인 개념으로 힙이나 다양한 다른 방법을 이용해 구현된다.
각 원소들은 우선순위를 갖고 우선순위 큐에서 높은 우선순위를 가진 원소가 낮은 우선순위를 가진 원소보다 먼저 처리된다.
즉, 임의의 순서로 삽입되지만, 정해진 순서로 삭제된다.
- push() : 하나의 원소를 우선순위를 지정하여 추가
- pop() : 가장 높은 우선순위를 가진 원소를 큐에서 제거 후 반환
1. 우선순위 큐 구현해보기(최소힙으로 구현)
class PriorityQueue :
def __init__(self) :
# 여기서 사용할 리스트는 완전 이진트리를 구현
# 0번 인덱스를 사용하지 않기 위해 0번에 None 삽입
self.items = [None]
def __len__(self) :
return len(self.items) - 1
def __repr__(self) :
# 우선순위 큐 안에 값을 확인하기 위한 함수
return ' '.join(map(str, self.items[1:]))
def __percolate_up(self) :
# 현재 가장 마지막 인덱스 = 방금 삽입한 원소의 인덱스
i = len(self)
parent = i // 2
while i > 1 :
# 가장 작은 수를 우선순위가 높은 것으로 가정
# 만약 방금 삽입한 값이 부모노드보다 값이 작으면 변경
if self.items[parent] > self.items[i] :
self.items[parent], self.items[i] = self.items[i], self.items[parent]
i = parent
parent //= 2
def heappush(self, item) :
# 배열의 맨 뒤에 뭔소 삽입 후 위치 조정
self.items.append(item)
self.__percolate_up()
def __percolate_down(self, idx = 1) :
# 비트연산자 사용 -> left는 부모 인덱스에 X2, right는 부모 인덱스에 X2+1
# 1번 부터 사용하기 때문에 위와 같은 식으로 자식 노드의 인덱스를 구한다.
left, right = idx << 1, idx << 1|1
smallest = idx
# 현재 인덱스보다 왼쪽 자식 인덱스의 값이 작을 경우
if left < len(self) and self.items[left] < self.items[smallest] :
smallest = left
# 현재 인덱스보다 오른쪽 자식 인덱스의 값이 작을 경우
if right < len(self) and self.items[right] < self.items[smallest] :
smallest = right
# 현재 인덱스와 가장 작은 값의 인덱스를 저장한 값과 다를 경우
if smallest != idx :
self.items[idx], self.items[smallest] = self.items[smallest], self.items[idx]
self.__percolate_down(smallest)
def heappop(self) :
result = self.items[1]
# 가장 마지막에 있는 값을 root로 이동 후 pop() 수행-> 위치 조정
self.items[1] = self.items[-1]
self.items.pop()
self.__percolate_down()
return result
# 이 코드를 main으로 실행할 경우에만 실행된다.
if __name__ == '__main__' :
q = PriorityQueue()
nums = [15, 20, 30, 35, 25]
for num in nums:
q.heappush(num)
print('초기 priority queue')
print(q)
q.heappush(9)
print('\nheappush 연산 후 priority queue')
print(q)
print('\nheappop 연산 후 priority queue')
print('\nheappop 반환값: ', q.heappop())
print(q)
※ 비트 연산자 : 비트 단위로 연산을 수행한다 ※

위의 이미지에서 0b : 이진수를 뜻한다.

<< 연산자 : 오른쪽에 1개의 0을 추가한다. (1 << 1 → 10 = 2)
| 연산자 : or 연산 (2 | 1 → 10|01 → 11 = 3)
구현 코드 참고 블로그
https://koosco.tistory.com/112
[자료구조] 우선순위 큐(Priority Queue)
1. 우선순위 큐 - 우선순위 큐는 각 원소들이 우선순위를 갖고 있는 추상 자료형이다. - FIFO 구조를 갖는 큐와 다르게 우선순위 큐는 들어온 순서와 상관없이 우선순위가 높은 원소가 먼저 나간다
koosco.tistory.com
2. PriortyQueue 모듈 사용
from queue import PriorityQueue
# queue 만들기
q = PriorityQueue()
q2 = PriorityQueue(maxsize=10) # 큐의 사이즈 지정 가능
# 큐에 값 삽입
q.put(3)
q.put(4)
q.put(1)
q2.put((2, 'one')) # 우선순위를 지정하여 값 삽입 가능
q2.put((3, 'two'))
q2.put((1, 'three'))
# 큐에서 값 제거
print(q.get())
print(q2.get())
3. Heapq 모듈 사용 (최소힙)
import heapq
# 힙으로 사용할 리스트
h = []
# 힙 push
heapq.heappush(h, 4)
heapq.heappush(h, 3)
heapq.heappush(h, 1)
heapq.heappush(h, 2)
# 힙 pop
print(heapq.heappop(h))
# 리스트를 제자리에서 heap으로 변경하는 함수
x = [4, 3, 1, 2, 5, 6]
print(x)
heapq.heapify(x)
print(x)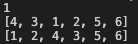
4. 우선 순위 큐 관련 백준 문제 풀이
import sys
max_heap = [0]
def push(v) :
max_heap.append(v)
i = len(max_heap)-1
parent = i // 2
while i > 1 :
if max_heap[parent] < max_heap[i] :
max_heap[parent], max_heap[i] = max_heap[i], max_heap[parent]
i = parent
parent //= 2
def down(idx) :
left, right = idx*2, idx*2+1
s = idx
if left < len(max_heap) and max_heap[left] > max_heap[s] :
s = left
if right < len(max_heap) and max_heap[right] > max_heap[s] :
s = right
if s != idx :
max_heap[idx], max_heap[s] = max_heap[s], max_heap[idx]
down(s)
def heappop() :
result = max_heap[1]
max_heap[1] = max_heap[-1]
max_heap.pop()
down(1)
return result
N = int(sys.stdin.readline())
for _ in range(N) :
i = int(sys.stdin.readline())
if i == 0 :
if len(max_heap) == 1 :
print(max_heap[0])
else :
print(heappop())
else :
push(i)공부할 겸 힙 모듈을 사용하지 않고 최대힙을 구현해 보았다.
import sys
import heapq
N = int(sys.stdin.readline())
min_heap = [] # 중간값보다 작은 값들이 들어갈 우선순위 큐 - 최대힙
max_heap = [] # 중간값보다 큰 값들이 들어갈 우선순위 큐 - 최소힙
for _ in range(N) :
num = int(sys.stdin.readline())
if len(min_heap) == len(max_heap) :
heapq.heappush(min_heap, -num) # 최대힙으로 사용하기 위해 값에 - 사용
else :
heapq.heappush(max_heap, num)
# 수의 개수가 짝수개라면 중간에 있는 두 수 중에서 작은 수
# 즉, min_heap이 중간값을 가지고 있도록 해야한다.
if max_heap and max_heap[0] < -min_heap[0] :
left = heapq.heappop(min_heap)
right = heapq.heappop(max_heap)
heapq.heappush(min_heap, -right)
heapq.heappush(max_heap, -left)
print(-min_heap[0])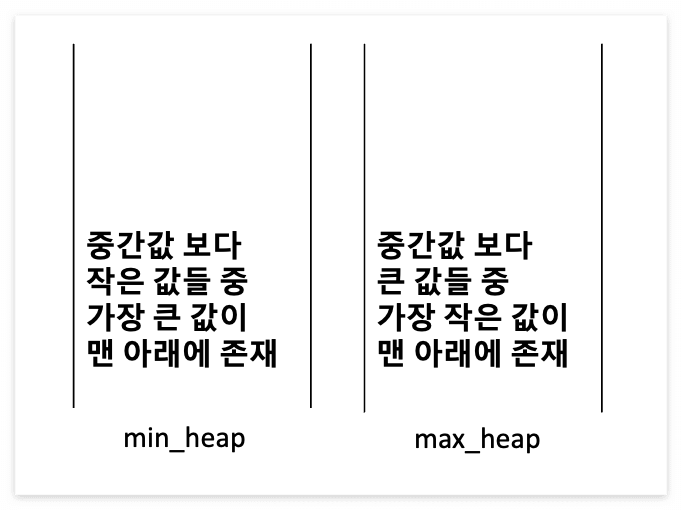
힙을 2개를 사용하여 중간값을 기준으로 나눈다.
▶ min_heap : 중간값 보다 작은 값들을 최대힙에 저장
▶ max_heap : 중간값 보다 큰 값들을 최소힙에 저장
문제 조건 : 백준이가 외친 수의 개수가 짝수개라면 중간에 있는 두 수 중에서 작은 수를 말해야 한다.
그래서 각 힙에는 중간값이 0번 인덱스에 존재하도록 만들고 그 중에서 min_heap 힙에 더 작은 값을 갖도록 한다.
<참고 블로그> https://hongcoding.tistory.com/93
import sys
import heapq
N = int(sys.stdin.readline())
def getScore() :
card = []
score = 0
for _ in range(N) :
heapq.heappush(card, int(sys.stdin.readline()))
while len(card) > 1 :
n1 = heapq.heappop(card) # 최솟값1
n2 = heapq.heappop(card) # 최솟값2
score += (n1+n2) # 현재까지 비교 횟수 누적 저장
# 위의 합을 힙에 추가
# 후에 다른 카드와 비교할 때 필요
heapq.heappush(card, n1+n2)
print(score)
getScore()처음에는 최대힙을 사용하여 들어온 두 값을 더하고 이를 힙에 같이 저장하는 방식으로 할려고 했다.
그러나 들어오는 순서가 작은 값들 부터 들어온다는 보장이 되어있지도 않고 이 방식은 힙을 사용하지 않고도 똑같이 구현할 수 있었다.
또한 전혀 최솟값을 구할 수 있는 방식이 아니었다.
그래서 바꾼 것은 우선 최소힙을 사용하기로 결정했다.
1. 최솟값 2개를 pop
2. 합을 구하고 누적저장 + 힙에 삽입
3. 힙에 요소가 2개 이상 남을 경우에만 1,2를 반복한다.
누적해서 더해야 하기 때문에 초반에 작은 것이 유리하므로 이와 같은 방식을 선택했다.
import sys
import heapq
# https://velog.io/@piopiop/백준-13334-철로파이썬 참고
########input 값##########################################################
N = int(sys.stdin.readline())
tmp = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
# 철로 길이
d = int(sys.stdin.readline())
roads = []
# 입력받은 집,회사 사이의 거리가 철로 길이보다 긴 경우 제외 -> 애초에 포함될 수 없기에 상관없음
for i in tmp :
i.sort()
if i[1] - i[0] <= d :
roads.append(i)
roads.sort(key= lambda x : x[1])
############################################################################
count = 0
heap = [] # 현재 위치에서 철로 길이 안에 포함된 좌표 저장
for r in roads :
if not heap :
heapq.heappush(heap, r)
else :
# 현재 보고 있는 r의 오른쪽 좌표에서 d만큼 뺀 값 = 철로 시작점
# 현재 힙 안의 최솟값의 시작점이 위의 값보다 작으면 철로에 포함되지 않는다.
while heap[0][0] < r[1] - d :
heapq.heappop(heap)
if not heap :
break
heapq.heappush(heap, r)
# 최댓값 저장
count = max(count, len(heap))
print(count)솔직히 어떻게 문제를 풀어야할지 감이 전혀 안잡혔다.
완전탐색을 해야할 것 같은데 그것도 구현하기 어려웠다. 그래서 블로그를 참고하여 알고리즘을 찾아보았다.
<참고 블로그> https://velog.io/@piopiop/백준-13334-철로파이썬
내가 너무 힙을 사용할 방법을 생각하지 못했었다.
최소힙으로 저장하면 좌표들은 시작점이 앞에 있는 것부터 정렬되므로 철로의 끝점을 변경해가면서 철로의 길이 안에 포함되어 있지 않을
경우에 힙에서 제거를 해주면 힙에는 현재 철로 위치에서 포함되는 좌표만 들어가 있게 된다.
정말 문제를 각 좌표 사이의 거리, 좌표의 빈도 등 다양하게 생각해봤지만, 사용할 수 없었다. 진짜 늘 느끼지만 연습을 많이 해야겠다.
728x90
'KraftonJungle2기 > Today I Learned' 카테고리의 다른 글
| [TIL] 스택계산기 + Hashing3 (0) | 2023.04.19 |
|---|---|
| [TIL] 분할 정복 연습문제 풀이 + Hashing2 (0) | 2023.04.18 |
| [TIL] 백준 풀이 정리2 (0) | 2023.04.16 |
| [TIL] 자료구조 - Queue + Hashing이란? (0) | 2023.04.15 |
| [TIL] Algorithm - 분할정복 + 스택 (0) | 2023.04.14 |


