1. 분할 정복 연습문제
1. 10830번 - 행렬 제곱
import sys
N, B = map(int, sys.stdin.readline().split())
p = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
# 두 행렬을 곱하는 함수
def mul (a, b) :
result = [[0] * N for _ in range(N)]
for r in range(N) :
for c in range(N) :
for i in range(N) :
result[r][c] += a[r][i] * b[i][c]
result[r][c] %= 1000
return result
# 제곱근을 분할하는 함수
def getResult(p, b) :
if b == 1 :
for i in range(N) :
for j in range(N) :
p[i][j] %= 1000
return p
else :
tmp = getResult(p, b//2)
if b % 2 == 0 :
return mul(tmp, tmp)
else :
return mul(mul(tmp, tmp), p)
ans = getResult(p, B)
for a in ans :
# unpacking
print(*a)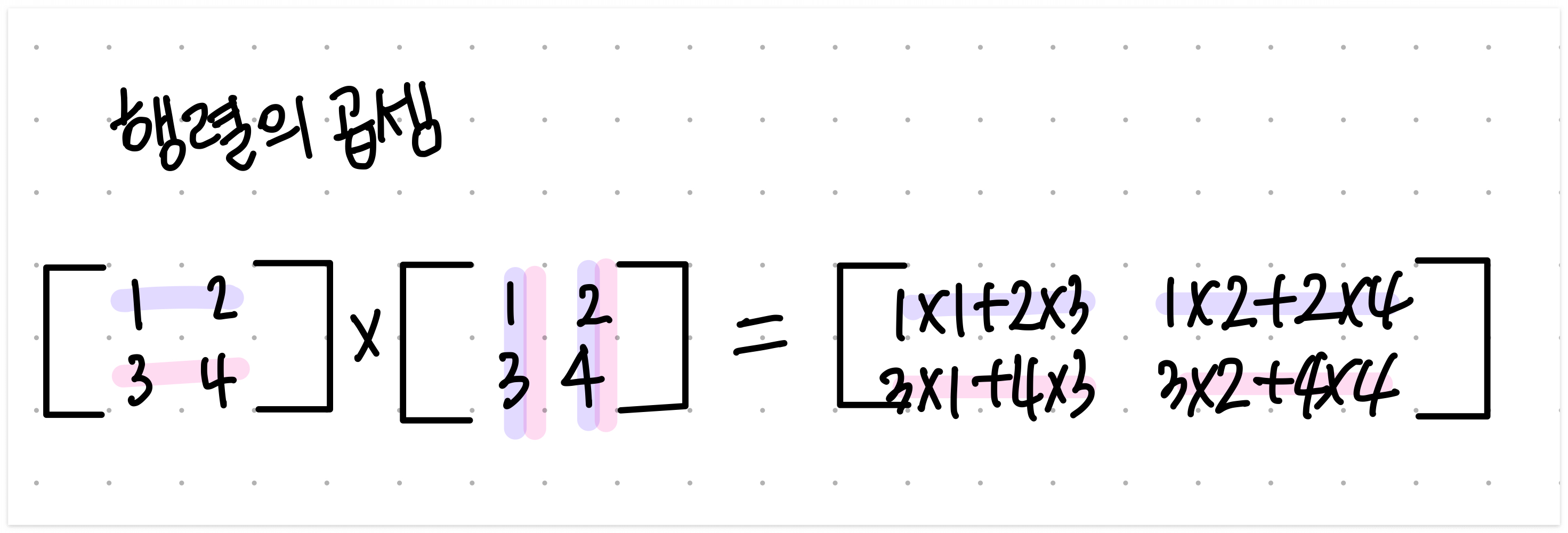
행렬의 곱셈은 헷갈리기는 하지만 어느 정도 구현할 수 있었다.
그리고 또다른 분할 문제를 푼 적이 있어서 코드를 작성하기 수월했다.
그러나 여기서 문제는 저장한 result 이차원 배열에서 한줄의 값들이 다른 줄에 계속해서 저장 되어서 나온다는 것이었다.
list1 = [[0]*2]*2
list2 = [[0]*2 for _ in range(2)]위의 두 코드는 모두 [[0,0], [0,0]] 2차원 배열을 만든다.
내가 mul() 함수에서 result를 초기화했던 방식도 list1과 같은 방식으로 했다.
그러나 여기서 위의 두 코드의 다른 점은 배열의 주솟값을 찾아보면 알 수 있다.

list1의 방식은 list1[0] = list1[1] 의 주솟값이 같다. 즉, 같은 주소의 배열을 참조하고 있어 값이 같이 변경된다.
list2의 방식은 list2[0] != list2[1] , 주솟값이 같지 않다. 즉, 서로 다른 배열이라는 의미이다.
이와 같이 어떻게 초기화하냐에 따라 문제가 발생할 수 있다는 것을 알았다.
★ unpacking (*)★
: 함수를 호출할 때 인자를 해체하는 개념
현재는 리스트의 값만 추출하고 싶어서 사용해보았다. 예전에는 반복문을 돌면서 값을 하나씩 출력해줬는데 편리하다.
3) packing, unpacking
`print`함수는 출력하고자하는 객체가 몇개던지, 즉 몇개의 인자를 받던지 상관하지 않고 출력해줍니다. ``` print(가나다 abc 123) print(가나다…
wikidocs.net
2. 6549번 - 히스토그램에서 가장 큰 직사각형
import sys
def rectangle(l, r) :
global histogram
# l,r 이 같은 값을 가리킬 경우 즉, 한개의 히스토그램만 남았을 경우
# 그 직사각형의 높이가 넓이이다.
if l == r :
return histogram[l]
mid = (l+r)//2 # 현재 가운데 원소
# 왼쪽 부분과 오른쪽 부분을 분할하여 직사각형의 넓이를 구하면서 큰 값을 area에 저장
area = max(rectangle(l, mid), rectangle(mid+1, r))
new_left = mid # 왼쪽에서 시작할 시작점 -> l에 맞닿을 때까지 -1
new_right = mid+1 # 오른쪽에서 시작할 시작점 -> r에 맞닿을 때까지 +1
height = min(histogram[new_left], histogram[new_right]) # 붙어있는 new_left와 new_right 중 낮은 높이 선택 -> 직사각형 연결
'''
1. 현재 경계부분이 아닌 왼쪽 또는 오른쪽 부분에서 구한 넓이가 최대인 경우 (코드 10번 줄 참고)
2. 현재 경계를 기준으로 new_left와 new_right로 만든 직사각형의 넓이가 최대인 경우
3. 경계의 왼쪽에서 너비 1의 직사각형이 최대인 경우
4. 경계의 오른쪽에서 너비 1의 직사각형이 최대인 경우
'''
area = max(area, height*2, histogram[new_left], histogram[new_right])
while l < new_left or new_right < r : # 범위 내일 경우
# 오른쪽 부분이 더 클 경우
if new_right < r and (new_left <= l or histogram[new_left-1] < histogram[new_right+1]) :
new_right += 1
height = min(height, histogram[new_right])
else :
new_left -= 1
height = min(height, histogram[new_left])
# new_right - new_left + 1 = width 즉, 직사각형의 너비
area = max(area, height*(new_right-new_left+1))
return area
while True :
n, *histogram = map(int, sys.stdin.readline().split())
if n == 0 :
break
print(rectangle(0, n-1))우선 이 문제는 몇 시간동안 공부하면서 분석을 해보았지만 정말 어려웠다. 풀었다기 보다 다른 사람의 풀이를 해석만 한 수준,,ㅠㅜ
<참고 블로그>
1. https://jih3508.tistory.com/75
2. https://velog.io/@piopiop/백준-6549-히스토그램에서-가장-큰-직사각형파이썬
3. https://aodtns.tistory.com/45
지난 번에는 스택으로 풀어보았는데 그때도 이해하기 어려웠지만 이 방법보다는 쉬웠다.
그래도 분할 정복이라는 방식이 어떻게 사용되는지에 대한 알고리즘은 알 수 있었다.
3. 2261번 - 가장 가까운 두 점
import sys
n = int(sys.stdin.readline())
spot = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]
spot.sort()
# 주어진 두 점 사이의 거리 구하는 함수
# 문제의 정답상 거리의 제곱을 구해야 하므로!
def distance(a, b) :
return (a[0]-b[0])**2 + (a[1]-b[1])**2
def fun(start, end) :
if start == end : # 같으면 거리 계산 불가능
return sys.maxsize
elif end - start == 1 : # 단 두점만 가지고 있으면 거리 반환
return distance(spot[start], spot[end])
else : # 분할
mid = (start+end) // 2
# mid를 기준으로 왼쪽 부분과 오른쪽 부분 계산하여 작은 길이 저장
tmp = min(fun(start, mid), fun(mid, end))
# 쪼개지는 부분 검증
candidate = []
# mid를 기준으로 mid-tmp ~ mid+tmp 범위 내에 존재하는 값을 후보자로 등록
for i in range(start, end+1) :
if (spot[mid][0]-spot[i][0]) ** 2 < tmp :
candidate.append(spot[i])
# y값을 기준으로 정렬
candidate.sort(key=lambda x: x[1])
# 후보 위치 중에서 범위 내에 존재하면 길이를 구하고 비교
for i in range(len(candidate)-1) :
for j in range(i+1, len(candidate)) :
if (candidate[i][1]-candidate[j][1])**2 < tmp :
tmp = min(tmp, distance(candidate[i], candidate[j]))
else :
break
return tmp
print(fun(0, n-1))문제는 이해가 되지만 구현이 어려웠던 문제였다.
분할 : 탐색 범위 분할
정복 : 탐색 범위가 0 인 경우, 1인 경우 계산하여 반환
결합 : tmp에 저장하면서 최솟값을 계속해서 업데이트
<참고 블로그>
1. https://velog.io/@e_juhee/python-백준-2261-가장-가까운-두-점
2. https://velog.io/@piopiop/백준-2261-가장-가까운-두-점파이썬
이번 주 알고리즘 중에서 가장 어려웠던 것은 분할 정복이었다.
분할하여 푸는 방식은 이해했는데 구현이 제일 힘들었다. 앞으로 좀 더 연습해야겠다.
2. Hash Table
매우 빠른 평균 삽입, 삭제, 탐색 연산 제공
1. Hash Function
① Perfect hash function
: key와 slot이 1:1 매칭이 되는 해시 함수, 실제로는 many to one 대응이기 때문에 현실적으로 불가능한 이상적인 해시 함수
② Universal hash function
: 서로 다른 값 x, y에 대해, F(x) == F(y) 일 확률이 1 / 해시테이블의 크기 보다 작다는 조건을 만족하면 universal hash function

③ Division hash function
: 나머지 연산을 사용한 해시 함수

이 외에 C-universal, Multiplication, Folding, Extraction hash function 등이 존재한다.
또한 key 값이 문자열일 경우 Additive, Rotating, Universal hash function 등이 존재한다.
이에 대한 자세한 설명은 아래의 링크 참고
https://velog.io/@ybw903/자료구조-해시테이블
[자료구조] 해시테이블
해시테이블 매우 빠른 평균 삽입,삭제,탐색 연산을 제공하는 자료구조입니다. 만약 해시테이블이 아닌 List에 Key와 Value쌍으로 저장하면 무엇이 문제일까? 중간요소가 삭제된 List의 탐색, 삽입,삭
velog.io
★ 좋은 해시 함수 ★
1. less collision (적은 충돌)
2. fast computation (빠른 계산)
을 만족하는 해시 함수이다.

2. Collision Resolution Method (충돌 회피 방법) : 간단한 개념 정리
- Open Addressing
- Linear Probing
- 현재 매핑된 키에 충돌이 발생하면 밑에 있는 슬롯을 확인한다.
- 즉, 한칸씩 내려가면서 빈칸이 나타나면 그곳에 값 저장
- quadratic probing
- double hashing
- Linear Probing
- Chaining
linear probing youtube 강의
https://www.youtube.com/watch?v=Bj4pd9rJp5c&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=19
현재 그냥 이정도 있다는 정도만 알고있다. 다음에 좀 더 공부해서 정리해서 올려야 겠다.
'KraftonJungle2기 > Today I Learned' 카테고리의 다른 글
| [TIL] Graph + 트리 순회 (0) | 2023.04.20 |
|---|---|
| [TIL] 스택계산기 + Hashing3 (0) | 2023.04.19 |
| [TIL] 자료구조 - 우선순위 큐 (0) | 2023.04.17 |
| [TIL] 백준 풀이 정리2 (0) | 2023.04.16 |
| [TIL] 자료구조 - Queue + Hashing이란? (0) | 2023.04.15 |


