1. 스택을 이용한 계산기
1. 식 표기법
- 전위 표기법(prefix, 폴란드 표기법) : 연산자를 연산 대상의 앞에 쓰는 연산 표기법
- ex) *+234
- 장점 : 프로그래밍 언어의 인터프리터에 의해 수학적 표현식에 대한 문법으로써 사용되는 경우,
곧바로 추상 문법 트리로 구문 분석되며, 사실 동일하게 전단사 함수를 정의할 수 있다. - 단점 : 사람의 눈으로 쉽게 이해하거나 계산하기 힘들다.
- 중위 표기법(infix) : 연산 대상 사이에 연산자를 쓰는 연산 표기법
- ex) (2+3)*4
- 장점 : 사람에게 친숙하다.
- 단점 : 우선 순위 규칙에 따라 연산 순서를 결정하여 괄호로 연산이 수행되는 의도된 순서를 가리키는데 필수적이다.
컴퓨터로 구문 분석하기 어렵다.
- 후위 표기법(postfix) : 연산자를 연산 대상의 뒤에 쓰는 연산 표기법
- ex) 23+4*
- 장점 : 특별한 변환이 필요없이 수식을 앞에서부터 읽어나가면서 스택에 저장하면 된다.
우선순위가 모호하지 않아 괄호가 필요하지 않다. - 단점 : 사람의 눈으로 쉽게 이해하거나 계산하기 힘들다.
2. 표기법 변환

★ 중위 표기법을 후위 표기법으로 변환하는 알고리즘 ★
# 중의 표현식 -> 후위 표현식으로 변환하는 함수
def convert_to_postfix(S):
opStack = ArrayStack() # 연산자를 저장할 스택
answer = ''
# 입력받은 식 반복
for w in S :
if w in prec : # 연산자일 경우
if opStack.isEmpty() : # 스택에 아무것도 없으면
opStack.push(w)
else :
if w == '(' :
opStack.push(w)
else :
# 현재 연산자의 우선순위가 스택의 top에 있는 연산자의 우선순위보다 크면 반복문 종료
# 연산자 우선순위가 높은 것 먼저 pop해야 한다.
while prec.get(w) <= prec.get(opStack.peek()) :
answer += opStack.pop()
if opStack.isEmpty() : break
opStack.push(w)
elif w == ')' :
# 짝이 맞는 열린 괄호가 나오기 전까지 앞에 있던 연산자들 pop
while opStack.peek() != '(' :
answer += opStack.pop()
opStack.pop()
else : # 피연산자일 경우
answer += w
print(f'answer: {answer}\topStack: {opStack.serialize()}')
# 식을 다 확인한 후 스택에 값이 비어질 때까지
while not opStack.isEmpty() :
answer += opStack.pop()
return answer
3. 계산 과정
- 피연산자 : 스택에 push
- 연산자 : 스택에서 pop()을 2번 실행하여 얻어진 피연산자를 이용해 연산 실행 → 연산 결과 스택에 push
- 주의할점 : 교환법칙이 성립하지 않는 뺄셈과 나눗셈!
- 스택은 후입선출 구조이기 때문에 첫번째 pop()한 값 = 두번째 인자, 두번째 pop()한 값 = 첫번째 인자이다.
# 계산 구현
# tokens : 후위표기법으로 표현된 식
def calculate(tokens):
stack = ArrayStack() # 피연산자들을 저장할 스택
for token in tokens:
if token == '+':
stack.push(stack.pop()+stack.pop())
elif token == '-': #교환 법칙 성립 안함
rv = stack.pop()
stack.push(stack.pop()-rv)
elif token == '*':
stack.push(stack.pop()*stack.pop())
elif token == '/': #교환 법칙 성립 안함
rv = stack.pop()
stack.push(stack.pop()//rv)
else: # 피연산자일 경우 stack에 push
stack.push(int(token))
return stack.pop() # 마지막 연산 결과 반환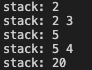
이와 같이 후위표기법을 이용한 계산은 수식을 읽어나가면서 바로바로 연산이 가능하다.
전체 코드
https://github.com/ChoSooBeen/PythonWorkspace/blob/main/StackExample/EX2_stack.py
GitHub - ChoSooBeen/PythonWorkspace
Contribute to ChoSooBeen/PythonWorkspace development by creating an account on GitHub.
github.com
참고
https://codingalzi.github.io/algopy/infix_prefix_postfix.html
3.2. 중위, 전위, 후위 표기법 — 문제해결 알고리즘
3.2. 중위, 전위, 후위 표기법 소스코드 아래 내용을 (구글 코랩) 중위/전위/후위 표기법에서 직접 실행할 수 있다. 주요 내용 중위/전위/후위 표기법 표기법 변환 알고리즘 후위 표현식 계산 알고
codingalzi.github.io
2. Collision Resolution Method
- Open Hashing(개방 해싱) : 주소 밖에 새로운 공간을 할당하여 문제 해결
- chaining(개방 해싱인 동시에 폐쇄 해싱)
- Closed Hashing(폐쇄 해싱) : 처음에 주어진 해시테이블 공간 안에서 문제 해결
- open addressing
- chaining
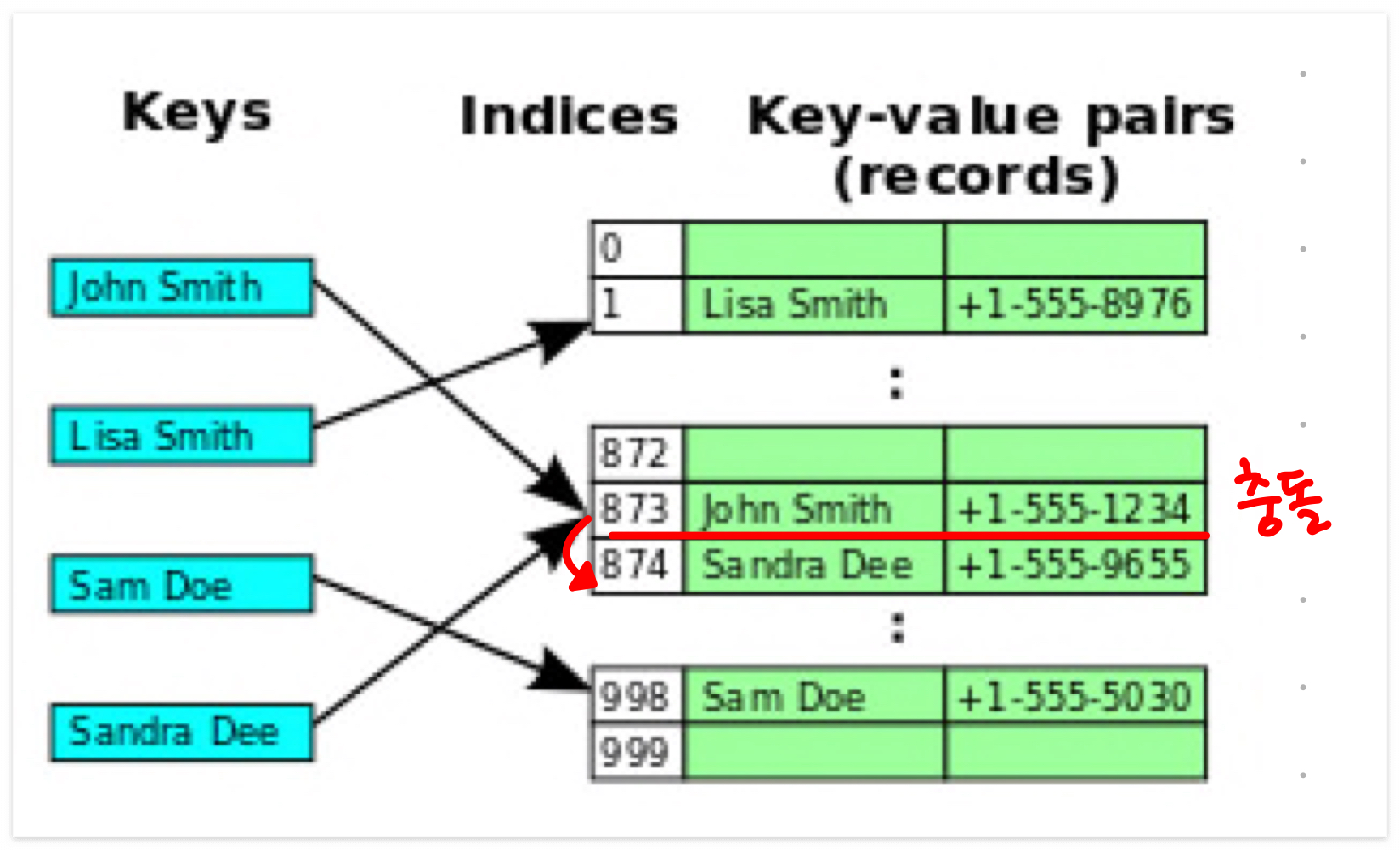
1. open addressing
충돌이 발생하면 주위의 빈칸을 찾아서(대체 위치 탐색) 값 삽입
- linear probing : 충돌하면 빈칸이 나타날 때까지 한칸씩 내려간다.
▶ 사용 연산 Pesudo-Code
find_slot(key) : key에 맞는 slot 번호 반환하는 함수

set(key, value) : 올바른 위치에 삽입

remove(key) : 해당 원소를 삭제하는 함수



- quadratic probing : 제곱근만큼 증가하면 빈칸 탐색

- double hashing : 2개의 해시함수를 사용하여 보조 해시함수만큼 증가하며 빈칸 탐색


▶ 성능
: 사용한 연산(set, remove, search)의 영향을 받는다.
이는 cluster size에 영향을 받는다. cluster size는 아래의 4가지 요소에 영향을 받는다.
- hash funtion : 키값을 얼마나 분산시키며 배치하는지
- collision resolution method : 충돌시 어떻게 대처하는지
- load factor : N/M
- N : 해시 테이블 H에 저장된 item 개수
- M : 해시 테이블 H의 크기
- 즉, 해시 테이블이 차있는 비율 - 0 <= N/M <= 1
- 1에 가까울수록 해시테이블이 많이 찼다.
- 0에 가까울수록 해시테이블이 많이 비어있다.

- 충돌 비율 : collision 횟수 / N
- 충돌횟수가 많아 질수록 cluster size는 커질 수 밖에 없다.
평균적으로 M >= 2N 즉, 최소 50%이상이 빈 슬롯을 유지할 경우
cluster 평균 크기 = O(1) = 평균 연산 O(1)
open addressing wiki
https://en.wikipedia.org/wiki/Open_addressing
Open addressing - Wikipedia
From Wikipedia, the free encyclopedia Hash collision resolution technique Hash collision resolved by linear probing (interval=1). Open addressing, or closed hashing, is a method of collision resolution in hash tables. With this method a hash collision is r
en.wikipedia.org
3. Chaining
: 각각의 슬롯마다 한방향 연결리스트가 존재하여 동이할 키값에 저장하는 방식

C로 구현한 chaining 기법
https://zoosso.tistory.com/872
[해시] Hash Chaining 기법 구현
[해시] Hash란?에 작성한 Hash를 구현하는 방식 중 하나인 체이닝(Chaining) 기법을 구현하였습니다. Hash 개념이 필요하신 분은 먼저 [해시] Hash란?을 참고해주세요 Chaining 기법 Hash Function이나 주어지는
zoosso.tistory.com
hash table 관련 사이트
http://wiki.hash.kr/index.php/해시테이블
해시테이블 - 해시넷
해시 테이블로 된 작은 전화 번호부 해시테이블(hash table)은 해시함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 인덱스 혹은 주소 삼아 데이터의 값(value)을 키와 함께 저장하여 검색을
wiki.hash.kr
'KraftonJungle2기 > Today I Learned' 카테고리의 다른 글
| [TIL] Algorithm - 최소 신장 트리 + 그래프 기본 문제 풀이 (1) | 2023.04.21 |
|---|---|
| [TIL] Graph + 트리 순회 (0) | 2023.04.20 |
| [TIL] 분할 정복 연습문제 풀이 + Hashing2 (0) | 2023.04.18 |
| [TIL] 자료구조 - 우선순위 큐 (0) | 2023.04.17 |
| [TIL] 백준 풀이 정리2 (0) | 2023.04.16 |



