1. 문제 풀이 정리
1. 16120번 - PPAP
import sys
s = sys.stdin.readline().strip()
stack = []
ppap = ["P", "P", "A", "P"]
for i in s :
stack.append(i)
# 현재 스택에 PPAP가 있으면 3번 pop하여 P만 남긴다.
if stack[-4:] == ppap :
stack.pop()
stack.pop()
stack.pop()
# 최종적으로 P만 남을 경우
if stack == ["P"] :
print("PPAP")
else :
print("NP")
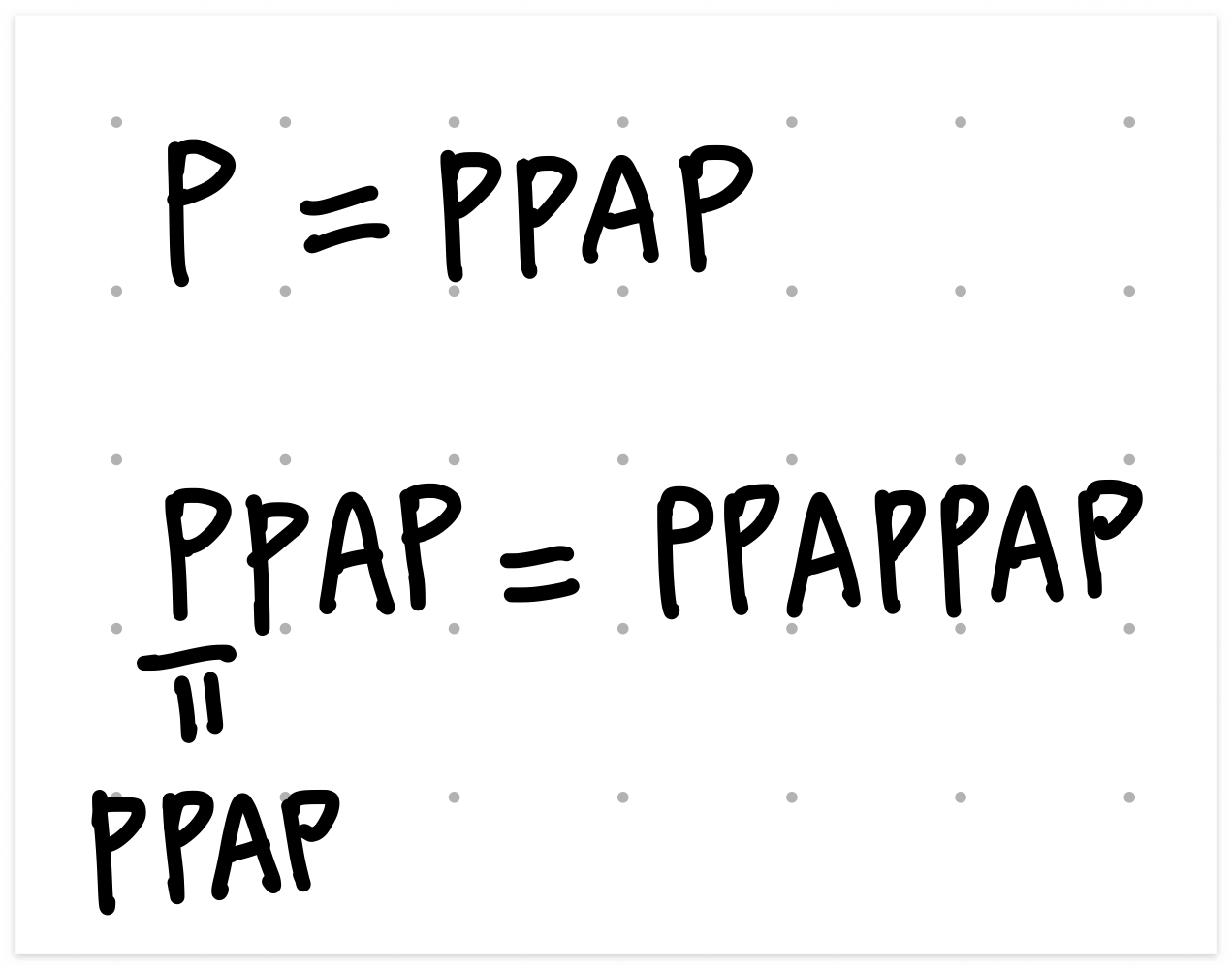
문제에서 조건을 보면 PPAP 는 P로 바꿀 수 있고 P 를 PPAP로 바꿀 수 있다.
즉, 어떤 문자열을 받고 이 문자열이 PPAP 문자열인지 확인하려면 PPAP인 경우에 모두 P로 변경하면서 문자열을 줄인다.
최종적으로 P만 남게 되면 PPAP 문자열이라고 생각할 수 있다.
이때 주의할 점은 입력받은 문자열에서 마지막 개행문자를 꼭 제거(strip())해줘야 답을 얻을 수 있다.
2. 5904번 - Moo 게임
import sys
# https://velog.io/@e_juhee/python-백준-5904-Moo-게임 참고
N = int(sys.stdin.readline())
total_length = 3 # 처음에는 moo 세글자
n = 0 # 몇번째 수열인지 = 문제상의 k -> 가운데 길이 구하기 위함
while total_length < N: # 전체 길이가 N보다 크거나 같아야지 N번째 값 확인 가능
# 기존 수열 * 2 + 3(moo) + 추가될 o의 개수(n)
n += 1
total_length = 2 * total_length + n + 3
def moo(n, total_length, mid_length) :
# n <= 3 이면
# moo 문자열에서 확인 가능
if n == 1 :
return 'm'
elif n <= 3 :
return 'o'
# n > 3
else :
# 가운데 수열을 제외하면 양쪽이 같다. 그리고 반으로 자른다.
# 즉, left는 s(k-1)
# right는 (moo+ k개의 o) + s(k-1)
left_length = (total_length - mid_length) // 2
if n <= left_length : # n이 왼쪽에 존재할 경우
return moo(n, left_length, mid_length-1)
if n > left_length + mid_length : # n이 오른쪽에 존재할 경우
# 범위를 줄인만큼 찾고자 하는 n의 크기도 줄인다.
# -> 왼쪽과 오른쪽은 문자열의 내용은 동일하고 인덱스번호만 다르다.
# 왼쪽 수열로 다시 함수를 실행한다.
return moo(n-left_length-mid_length, left_length, mid_length-1)
# 즉, n의 범위가 left_length < n <= left_length + mid_length 일 경우
# n이 mid에 존재할 경우
if n - left_length == 1 : # mid의 시작 부분일 경우
return 'm'
else :
return 'o'
# mid의 길이는 추가된 o의 개수 n과 moo의 길이 3을 더한 값이다.
print(moo(N, total_length, n+3))
입력되는 데이터값을 생각하지 않고 풀면 재귀로 단순하게 풀 수 있었다.
그러나 우리는 시간과 메모리가 제한되어있으므로 새로운 방식을 찾아야 했다.
솔직히 이 풀이를 이해하는데도 시간이 걸렸다. 그래도 시간을 가지고 하나씩 정리하고 분석하니 쉽게 이해할 수 있었다.
나중에 추가적으로 도전할 문제
https://www.acmicpc.net/problem/1933
1933번: 스카이라인
첫째 줄에 건물의 개수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 N개의 줄에는 N개의 건물에 대한 정보가 주어진다. 건물에 대한 정보는 세 정수 L, H, R로 나타나는데, 각각 건물의 왼쪽 x좌표, 높이, 오
www.acmicpc.net
2. Graph
G = (V, E) → V : 정점 / E : 간선
1. 그래프의 표현
1. 인접 리스트 표현(Adjacency-list representation)
- |E| < |V|^2 처럼 간선의 개수가 정점의 개수 제곱보다 훨씬 작은 작은 밀도 그래프일 때 효율적이다.
- |V| 개의 리스트의 배열 Adj로 구성되어 있고 각 리스트는 V에 들어있는 정점 하나에 대한 것이다.
- 각 u ∈ V 에 대해 Adj[u]는 간선 (u,v) ∈ E 가 존재하는 모든 정점 v를 포함한다.
- 즉, Adj[u]는 정점 u와 연결된 모든 정점들로 구성된다.
- 인접 리스트들의 길이의 총 합
- 방향 리스트 : |E| (u → v ≠ v → u)
- 무방향 리스트 : 2|E| (u → v = v → u)
- 필요한 메모리 : O(V + E)
- 장점 : 다른 변형된 형태의 그래프를 지원하기 위해 수정할 수 있다.
- 단점 : 주어진 간선(u, v)가 그래프에 존재하는지 확인하는 것이 인접 리스트 Adj[u] 에서 검색하는 것보다 빠를 수 없다.
2. 인접 행렬 표현
- |E| ≒ |V|^2 처럼 간선의 개수가 정점의 개수 제곱과 거의 비슷한 높은 밀도 그래프일 경우,
- 주어진 두 정점을 연결하는 간선이 존재하는지 빠르게 확인할 필요가 있을 경우에 효율적이다.
- 정점에 임의의 순서로 번호가 메겨져 있다고 가정하고 |V| × |V| 행렬 로 표현
- 필요한 메모리 : O(V^2)
- 무방향 그래프일 경우
- 주대각선(왼쪽 위에서 오른쪽 아래로 향하는 대각선) 기준으로 대칭
- 무방향 그래프의 인접행렬 A는 그 자신의 전치 행렬과 같다.
- 응용으로 대각선 또는 그 위쪽만 저장하여 필요한 메모리 용량을 절반 정도 줄일 수 있다.
- 장점 : 가중치가 없는 그래프에 대해 행렬 원소마다 한 비트만을 필요로 한다.
- 단점 : 인접 리스트보다 공간적인 면에서 비효율적이다.
그래프 개념 정리 : https://soo-note.tistory.com/19
java 로 구현한 그래프 : https://github.com/ChoSooBeen/graph
3. 트리 순회(Tree Traversal)
트리 구조에서 각각의 노드를 정확히 한번만 체계적인 방법으로 방문하는 과정
현재 노드를 방문하는 것, 왼쪽 자식 노드를 순회하는 것, 오른쪽 자식 노드를 순회하는 것 = 3가지 주요 단계
<참고> https://ko.wikipedia.org/wiki/트리_순회
1. 전위 순회(Preorder)

root → left → right 순으로 방문한다. 깊이 우선 순회(Depth-first traversal)라고도 한다.
2. 중위 순회

left → root → right 순으로 방문한다. 대칭 순회(Symmetric)이라고도 한다.
3. 후위 순회

left → right → root 순으로 방문한다.
< 순회 관련 문제 풀이 >
import sys
class node :
def __init__(self, root) :
self.root = root # 현재 노드
self.left = None # 왼쪽 자식 노드
self.right = None # 오른쪽 자식 노드
pre_result = ""
in_result = ""
post_result = ""
# 전위 순회
def preorder(n) :
global pre_result
pre_result += n.root
if n.left != None :
preorder(n.left)
if n.right != None :
preorder(n.right)
# 중위 순회
def inorder(n) :
global in_result
if n.left != None :
inorder(n.left)
in_result += n.root
if n.right != None :
inorder(n.right)
# 후위 순회
def postorder(n) :
global post_result
if n.left != None :
postorder(n.left)
if n.right != None :
postorder(n.right)
post_result += n.root
N = int(sys.stdin.readline()) # 노드의 개수
# A의 아스키 코드 = 65
# 노드는 A ~ Z 까지 가능
# tree = 노드들의 리스트
tree = [node(chr(i+65)) for i in range(N)]
for _ in range(N) :
root, left, right = sys.stdin.readline().strip().split()
# 자식 노드가 존재하면 연결해 주어야 한다.
if left != '.' and right != '.' : # 양쪽 자식 노드 모두 존재할 때
tree[ord(root)-65].left = tree[ord(left)-65]
tree[ord(root)-65].right = tree[ord(right)-65]
elif left == '.' and right == '.' : # 둘다 없을 때
continue
elif left == '.' : # 왼쪽 자식 노드만 없을 때 = 오른쪽 자식 노드만 존재
tree[ord(root)-65].right = tree[ord(right)-65]
else : # 오른쪽 자식 노드만 없을 때 = 왼쪽 자식 노드만 존재
tree[ord(root)-65].left = tree[ord(left)-65]
preorder(tree[0])
inorder(tree[0])
postorder(tree[0])
print(pre_result)
print(in_result)
print(post_result)노드 클래스를 만들어서 각각의 노드 생성
◆ root = 현재 노드 값
◆ left = 왼쪽 자식 노드 연결
◆ right = 오른쪽 자식 노드 연결
대신 노드들을 tree라는 리스트에 저장한다.
단, tree에서의 인덱스 i + 65는 아스키 코드로 변환하면 노드의 값이 된다.
그러면 ord(root)-65 = root의 아스키 코드 값에서 65를 빼면 리스트의 인덱스로 사용가능
파이썬으로 연결리스트 구현 참고
https://wikidocs.net/191324
003. 파이썬으로 연결 리스트 구현하기
## 연결 리스트의 구조와 특징 연결 리스트는 여러 곳의 자료를 연결한 것이다. 연결 리스트는 배열처럼 선형 자료 구조이지만, 연속한 메모리 위치에 값을 저장되지는 않는다. …
wikidocs.net
'KraftonJungle2기 > Today I Learned' 카테고리의 다른 글
| [TIL] 그래프 문제 문제 풀이 (0) | 2023.04.22 |
|---|---|
| [TIL] Algorithm - 최소 신장 트리 + 그래프 기본 문제 풀이 (1) | 2023.04.21 |
| [TIL] 스택계산기 + Hashing3 (0) | 2023.04.19 |
| [TIL] 분할 정복 연습문제 풀이 + Hashing2 (0) | 2023.04.18 |
| [TIL] 자료구조 - 우선순위 큐 (0) | 2023.04.17 |



